A keresztmetszet a labda sík
A keresztmetszet a labda sík
Tétel 20.3. Bármilyen síkja a labda rész egy kör. A központ ezt a kör egy láb a merőleges a gömb középpontjában a vágási sík.
Bizonyítás. Hagyja, - a vágási sík és O - központja a labdát (lásd 453.). Csepp a merőleges a labdát központ és a gépen jelöli O „bázis a merőleges.
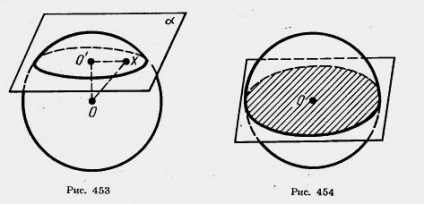
Legyen X - véletlen pont a világ, tulajdonosa a gépet. A Pitagorasz-tétel 2 = 0X 00 „2+ O'x 2. Mivel OX nem nagyobb, mint az R sugár a labdát, majd a. t. e., bármely keresztmetszeti síkja a labda pont az O pont „távolról nem nagyobb. Ezért tartozik a kör közepén O „és sugarát.
Ezzel szemben bármely pont a kör X a labdát. Ez azt jelenti, hogy a keresztmetszete a labda sík egy kör középpontja az O pont.” Ez azt bizonyítja, a tétel.
Az áthaladó sík közepén a labdát az úgynevezett középvonalától. A keresztmetszet a gömb közepén sík hívják a nagy kör (454 ábra.), Valamint a hatóköre részében - nagy kört.
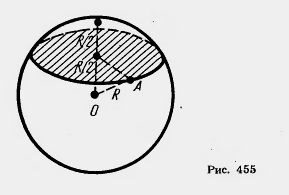
A probléma (30). Középen a labdát sugarú hajtjuk rá merőleges síkban. Mivel kapcsolódik a terület a kapott keresztmetszete területe a nagy körön?
Határozat. Ha a gömb sugara R (ábra. 455), akkor a kör sugara a keresztmetszete lesz
.
A terület aránya a kör területének nagy kör egyenlő
Pogorelov, geometria évfolyamon 7-11 tankönyv oktatási intézmények
Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.
Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.