Számítógépes aritmetikai - stadopedia alapjai
Bináris számtani, bináris műveletek táblája. A számok számtani műveletei lebegőpontos formában jelennek meg. A kivonás és a gép számkódjainak működése: közvetlen, fordított, kiegészítő.
Mielőtt folytatná a számítógépes lebegőpontos aritmetika tanulmányozását, vegye figyelembe a bináris aritmetikát a legegyszerűbb formában.
Bináris számtani. A számtani műveletek tetszőleges pozíciós számrendszerben bitenkénti, mint a decimális SS. Minden műveletnek saját tulajdonságai vannak. Így, ha két számot adunk hozzá, a magasabb rendbe való átjutás akkor fordulhat elő, ha a kibocsátási feltételek összege nagyobb vagy egyenlő, mint p - az SS alapja. A kivonáskor a legmagasabb szintről lehet kölcsönözni, ha a kibocsátás csökkenése kisebb, mint a levonható összeg. Nem szabad elfelejteni, hogy az alsó sorrendbe áthelyezett egység p. Ezeket a szabályokat bináris számrendszer esetén a táblázat tartalmazza. 12.1.
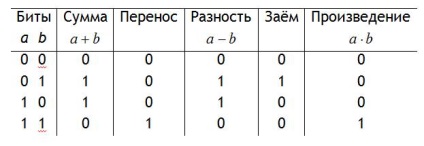
Figyelembe véve, hogy a nullához tartozó számok szorzása nulla értéket ad, és a szorzást egy az eredeti számmal adjuk meg, azt tapasztaljuk, hogy a bináris SS szorzása csökkenti az addíciót és a eltolás műveleteket, valamint a kivonás és eltolás műveleteit. Tekintsük ezeket a rendelkezéseket konkrét példákra.
12.1 példa. Számítsd ki az A és B számok összegét, különbségét és termékét, ahol A = 1010.011 (2). B = 100,101 (2). Számítsd ki a C.D hányadosát, ahol C = 11001 (2). D = 101 (2).
A "hitel" sorban az egység fölötti pont azt jelenti, hogy az egység alacsony sorrendben van elfoglalva. Az alsó sorrendbe való átmenet óta "fordul" a p. és p = 2 a mi esetünkben, akkor a megértés világossága érdekében íródott, bár ez nem teljesen helyes. Ha a kölcsönt tovább mozdítja, akkor a lemondó a kibocsátó egységben marad, a másik a következő alacsony sorrendbe kerül.
A számítógépekben ezeket a műveleteket úgy végzik, hogy figyelembe veszik a bit grid számának reprezentálását a sémák szerint, amelyek lehetővé teszik az elemi lépések számának minimalizálását, tovább tanulmányozhatjuk őket.
A számok számtani műveletei lebegőpontos formában jelennek meg. A lebegőpontos aritmetika végrehajtásának alapelve az, hogy a mantisszával és a megrendelésekkel végzett műveletek külön-külön és egymástól függetlenül készülnek.
Vegye figyelembe a lebegőpontos formában megjelenített számok hozzáadását és kivonását. Adjunk két pozitív számot a normalizált formában a számrendszerben b:
Mivel a pozíciószámrendszerekben történő addíció és kivonás bitenként történik, szükség van arra, hogy a terminusok mantissza azonos nevű bitjeinek méretei egybeesjenek. Ehhez az x1 és x2 számokat ugyanolyan sorrendbe kell hozni. A túlcsordulások elkerülése érdekében, a mantissza () korlátozásai miatt, a számokat egy nagyobb szám sorrendjébe kell sorolni. Feltéve, hogy definiteness, írunk
A fentiek szerint, amikor hozzáadja a lebegőpontos számokat (kivonja), a műveletek a következő sorrendben kerülnek végrehajtásra.
1. A megbízások összehangolása - a kisebb számok sorrendje a szám abszolút értékében nagyobb nagyságrenddel csökken, és a kisebb értéket a jobb oldalon a megbízások különbségével egyenlő számjegyek számával ().
2. A mantisszák kiegészítése (kivonása).
3. Kerekítés és normalizálás (ha szükséges) az eredmény.
Amellett. Vegyük például a két pozitív bináris szám hozzáadását.
12.2 példa. Számítsa ki a számok összegét, és reprezentálja őket lebegőpontos formában, feltéve, hogy a bitképben 5 bitet osztanak ki a mantissza ábrázolásnak, és a sorrendi ábrázolás 3 bit.
Írja be a számokat a normalizált formában
A bitképben így fog kinézni:
1. Rendelések összehangolása
2. A mantisszák (a jelzőhúrral együtt)
3. Kerekítés (1 a legmagasabb eldobott bitekhez)
A hatodik számjegy eldobásával kapunk egy lekerekített összegű mantisszát 0 11010.
4. Normalizálás (nem szükséges, mivel nem volt átvitel a mantisszából).
Kivonás. A kivonási művelet egy időigényesebb művelet a hozzáadottsághoz képest, mivel gyakran előfordul, hogy egy egységet a magasabb rendből kell venni. Ha kiderül, hogy a modulo kisebb, mint a pénzösszeg, akkor a hitelezési folyamat továbbra is a legmagasabb szintre esik, majd a kivonást újra végre kell hajtani, kicserélve a szubtrahendet és a csökkenést, valamint a különbség jeleit. Ugyanakkor algebrai szempontból a kivonás nem különbözik a hozzáadástól, és egy hozzáadás az ellenkező elemgel:
A kivonás műveletének egyszerűsítése és a kiegészítés csökkentése érdekében a gépkódok negatív számainak speciális ábrázolását alkalmazzuk.
Gépi kódok. A számok gépi kódjai három típusból állnak: közvetlen kód, kiegészítő és hátramenet.
Tekintsük az x számot. lebegőpontos formában:
Jelöljük annak mantissa R = 0, a1a2 ... an. Figyelembe véve a karakterek kódolására vonatkozó szabályokat, az FZ-ben való ábrázolása a következőképpen írható:
Ezt a reprezentációt az x szám közvetlen kódjának nevezzük. Mivel ezek a kifejezések átírhatók a formában
ebből következik, hogy a kivonási műveletet egy számmal ellátott addíciós művelettel helyettesíthetjük, majd ezt követően p. A kivonás ilyen módon történő végrehajtásához további kódot adunk meg az x számhoz:
Figyeljünk arra a tényre, hogy a negatív jel figyelembe vételével a kiegészítő kód a szám számának a számrendszerhez való hozzáadásával. azaz nem más, mint egy inverz elem a molekulák hozzáadásával a modulo p csoport gyűrűjében.
A kivonás mûködése más formában is megjelenhet:
Az ezzel a kapcsolattal definiált kód
az inverz számkódnak nevezzük. Ez a mantissza hozzáadás a maximális alapszámhoz.
A kapcsolatok (12.3) - (12.5) alapján arra a következtetésre juthatunk, hogy a vonal pozitív számai esetében az inverz és komplementer kódok egybeesnek a szám normalizált mantissal. Negatív számok (12.4) és (12.5) esetén az inverz és a kiegészítő kódokat összekötő kapcsolatot kapjuk meg:
amiből az következik, hogy ezek a kódok egymástól az utolsó számjegyben egyek. A további és inverz kódokat fordított kódoknak nevezzük. Vegyük észre, hogy definíció szerint a mantilla zéró egész szám. Ugyanakkor a szám jele nullával vagy a maximális alapszámmal van kódolva, és a mantissza előtt helyezkedik el. Így a szám teljes egészének és a megjelölés mentesítésének megfelelő mentesítés azonosítása a gépi kódokban történik.
Nézzünk három számot, és írjuk le gépi kódjaikat:
Figyelembe véve, hogy p a kalkulus p-rendszerében a 10 formában van, a további képleteket a (12.4) képlet alapján számoljuk ki. Az eredmény teljes része a kód aláírt számjegyéhez (szétválasztódik egy szóközzel):
Most számítsd ki az inverz kódokat:
Ne feledje, hogy a negatív bináris szám inverz kódjának megszerzéséhez egyszerűen csak 0-ra kell 1-re és 1-re váltani 0-val a közvetlen kódbeviteli számon.