Számítása elágazó láncok több forrásból
Ha az ismert áramköri elrendezés bonyolult, és meghatározott tulajdonságai minden az azt alkotó elemek, a számítás egy ilyen áramkör általában meghatározására korlátozódik az áramok az ágak és a csomópontok potenciálok. Ellentétben a fenti esetekben, elágazó lánc több forrásból igényel specifikus számítási módszerek. Megjegyezzük, hogy elágazó láncú, egyetlen forrásból, valamint lehet kiszámítani módszerekkel az alábbiakban tárgyaljuk.
Az ismeretlen áramok számával megegyező m ágakat. Ha néhány ág tartalmazza áramforrások, hogy ismeretlenek ezek az ágak megfelelő UJ. Így áramkör tervezés általában kell, hogy a független rendszer m egyenletek.
Módszer Kirchhoff egyenletek
Annak meghatározása, hogy az ismeretlen mennyiségek elkészítéséhez kapcsolódó és együttdöntési eljárás egyenletrendszert írt az I. és II Kirchhoff törvényei. Írni ezeket az egyenleteket kell előre számozott csomópontok hozzárendelésével mindegyiket a megfelelő érték a potenciális (1, 2, , n) és ágak, hogy az egyes aktuális értéke (I1, I2, lm) .
Mielőtt elkezdené írni az egyenleteket Kirchhoff törvények, be kell állítani a független egyenletek készül minden egyes ilyen törvényeket. Kirchhoff egyenlet poIzakonu. összekötő m ismeretlen áramok lehet rögzíteni az egyes áramköri csomópontok. Használata azonban közös megoldások csak n- 1 egyenletek, mint egyenletet írt az utolsó csomópont lesz az eredménye az előző egyenletek. PoIIzakonu Kirchhoff alkotják száma egyenletek számával megegyező m ágak mínusz a számú egyenlet áll Kirchhoff törvény I (n-1), azaz a p = m - (n - 1) = m - n + 1, ahol p - független áramkörök.
Mindezek az érvek érvényesek arra az esetre, amikor a jelenlegi források szerepelnek az áramkört. Ebben az esetben az ismeretlenek száma csökken áramot, de a megfelelő szám jelenik UJ feszültségeket. amely szerepelni fog az egyenlet az ismeretlen mennyiségek.
Így a számítási módszere az elágazó láncú nem tartalmazó áramforrások, a Kirchhoff következő egyenletekkel:
Jelöljük ág áramlatok, és válaszd a pozitív irány az önkényes.
Véletlenszerűen válasszon egy referencia-csomópont és több p = m - n + 1 független áramkörök.
Minden egység, kivéve a referencia, én meg egyenleteket Kirchhoff törvény. Az ilyen egyenletek kell lennie (n - 1).
Minden egyes kiválasztott kontúr képezik az egyenleteket Kirchhoff törvény II. Az ilyen egyenletek kell p.
Kirchhoff m egyenleteket m ismeretlenek rendszerrel áramok és megoldani közösen által meghatározott numerikus értékek az áramok.
Ha szükséges, kiszámított általánosított Ohm törvénye közötti feszültségkülönbség az ágak vagy csomópontok potenciálokat.
Helyességét a számítást a hatalmi egyensúlyt.
Ha qistochnikov áram az áramkörben. a helyes választás az összesített száma független hurkok össze megoldott egyenletet a rendszerben csökkenteni lehet q. Ha áramkörök úgy választjuk meg, hogy az egyes áramforrás lépett egyetlen áramkör megfelelő UJ belép csak egy egyenlet II Kirchhoff törvénye. Mivel az egyetlen ismeretleneket az áramok az (m - q) ágak, a számú egyenlet II Kirchhoff törvény lehet csökkenteni, hogy m - n + 1 - q. Ennek eredményeként, együtt (n - 1) egyenlet I. Kirchhoff-törvény, kapunk egy rendszer m - q egyenletek az ismeretlen áramok után együtt oldatok, amelyek q fennmaradó egyenletek meghatározásához használjuk.
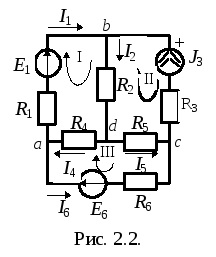
Jelöljük ág áramlatok.
Kiválasztása több független áramkörök (I, II, III) és a referencia csomópontban.
Egyenletek Kirchhoff törvény I.