Lépésről lépésre megoldást a problémára №10 - metszi a kör alakú henger és a tórusz


Lépésről lépésre megoldást a problémára №10 - metszi a kör alakú henger és a tórusz
Feladat № 10 is szentelt a téma építésének metszésvonala felületek - tórusz és a henger. Ez a legösszetettebb és munkaigényes feladatok, amelyek ismerete a módszereket építésének különböző felületei egyenesek metszéspontját.
Hogy oldja meg a problémákat, meg kell tudni:
- módszerek A felszíni komplex feladatok a rajzon;
- módszerek építésére metszésvonala felületek ábrázoló geometria feladatok:
a) A módszer a vágási sík;
b) eljárás esetén;
c) az alkalmazás labdát közvetítő (koncentrikus és excentrikus golyók).
Az eljárás megoldására probléma
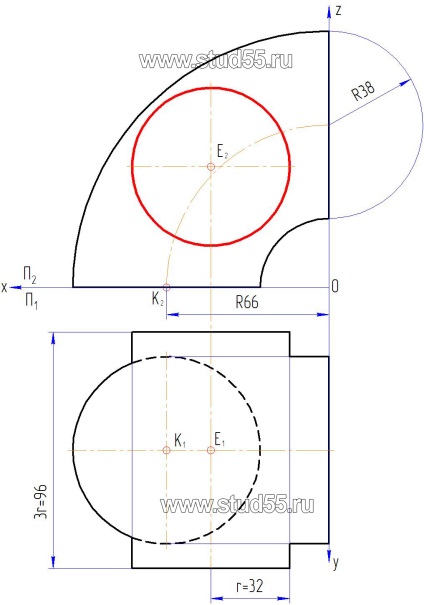
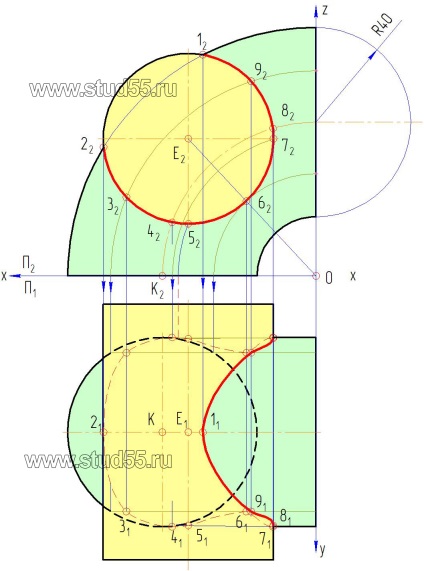
1. A találmány egy megvalósítási módja szerint hozzárendelés koordináta pontok építeni felszínére két kiálló egy jobbmenetes henger és a nyitott-tórusz (negyedik rész) a finom vonalak vagy ábrán. 10.1.
2. A konstrukció metszésvonal a generátorok módszert használhat, (módszer cutplane korábban ismertetett), a legmegfelelőbb tekintetében ezt a problémát. Ennek lényege abban a tényben rejlik, hogy a felszínen, amely a bemutatott általános formában, számos generátorok, jelzett a metszéspontja a generátorok a második felület, amely adott metszésvonal ezen felületek (ez egy első kiálló). Továbbá ezek a nyúlványok alakítás és vetítés elhelyezkedő pontok azokat a konjugált síkjában vetítés. Egyesítve sima vonal, megkapjuk a kívánt metszésvonal az adott felületre.
Tehát a probléma szükséges megépíteni a metszésvonal egy jobbmenetes henger és egy tórusz felülete (egy-negyedik nyitott tórusz). A probléma megoldódott, a következő sorrendben:
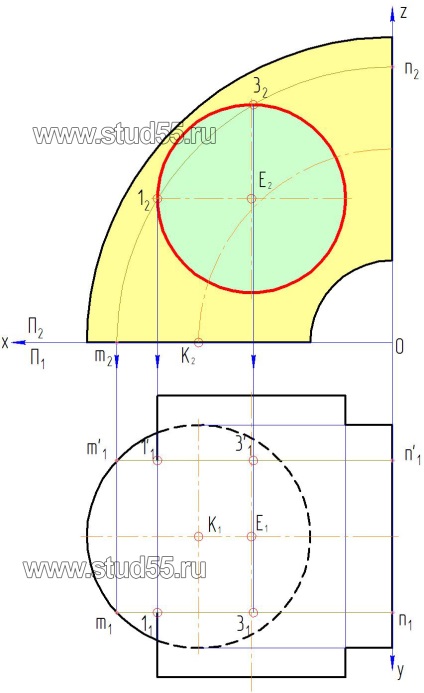
a) kialakítunk egy első vezető m2n2 frontális síkban P2 a nyúlványok a felszínen a tórusz. Megjegyezzük, a vetítési pontok keresztezi a hengeres 12 felület és a 32 = 1/2 = 3/2. Mivel 12 pont veszi az érintkezési pont a hengeres felületével a bal szélső alkotó tórusz (lásd 10.2 ábra ..);
c) átvitele (kiálló) a metszéspont az alkotója a hengeres felülete a frontális síkban, hogy a vízszintes síkban, megkapjuk a 12. és 32. -1'2 -3'2. Ez a vetítési pontok tartozó metszésvonala felületek, mint Mindketten tartoznak (a) a tórusz és a hengeres felületek.
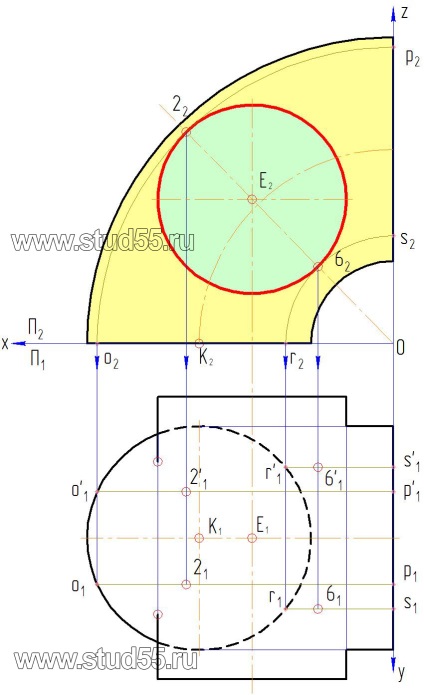
A következő két pont két pár képező huzalok o2p2ir2s2 a tetején és alján egy hengeres felülettel tangensét egy pont a 22. és 62.. Ahhoz, hogy a kiálló pont a P2. Meg kell át az előrejelzési központ 0 és E2 felhívni egy egyenes vonal, és olyan helyeken, ahol keresztezi a kontúr a felülete a henger, megkapjuk a kívánt vetítési pont 2. és 6. Ismételje a lépéseket bekezdésben meghatározott „a”, „b”, „c”.
d) kialakítunk egy további vezető keresztül keresztül a kiválasztott intervallum, vagy specifikus (referencia) pontja a felületek, ebben a példában keresztül alátámasztási pontok (ábra. 10.3).
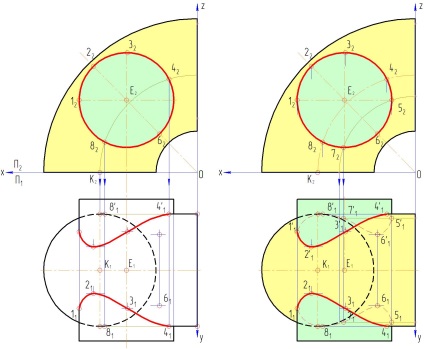
3. A vetítés pontot kapott a vízszintes síkban sorba vannak kötve a páros és páratlan ágak egy sima görbe alapján jelennek meg egyszerre mindkét oldalát - ez a metszésvonalnak meghatározott felületeken. Láthatóság azt állapítjuk meg a tényen alapul, hogy a pontok minden látható pont a vízszintes vetülete a hengeres felület, amely nyúlványok találhatók az elülső henger fölé átmérője. A tórusz látható felület fog mutatni egy vízszintes vetülete, amely elöl - fölött található, és a bal oldalon a tórusz tengely (tengelye a tórusz, valamint a henger átmérője a határait a láthatóság). A fennmaradó pontot egy henger és láthatatlan lesz a tórusz (ábra. 10.4).
4. Meg kell jegyezni, mint már említettük, hogy a kereszteződésekben a felületek lehet teljes vagy hiányos. Hiányos kereszteződés - a határvonalat átlépő van egy zárt hurok (a fenti példában a probléma), a teljes kereszteződés - a határvonalat átlépő osztja több zárt hurkok (többnyire két). Építési őket végezzük azonos módon megfogalmazott ezt a feladatot.
Kialakítása után metszésvonal felületek teljesen visszahúzott szintvonalak a látható része a metszésvonal és az egyes kontúrok a látható felület; láthatatlan (szaggatott) vonalak lemerült az összes többi sort.
Cím: Ábrázoló geometria /