Hogyan lehet megosztani mátrix
Lyta mátrix skaláris értéket. Bár a szétválás a mátrix egy másik mátrix nem szigorúan meghatározott, a mátrix mindig osztható skalár értéket. Ez a felosztás a szétválás minden egyes eleme a mátrix egy adott számot.
Matrix - vektor matematikai objektumok, amely két vagy több skalár elemét. Mátrixokat arra használjuk, hogy megtalálja sok ismeretlenes a rendszerben skalár egyenletek, valamint a műveletek nagy tömbök a számok. Mint a skalár értéket (például 1, 2, 3, 4) a vektorok végezhet matematikai számításokat, mint összeadás, kivonás és szorzás. Azonban a mátrixot nem lehet közvetlenül szét egymáshoz. Felosztására mátrixok kell végezni egy műveletet, amely két részből áll. Kezdetben meghatározni az inverz osztó (nevező). Akkor ez a mátrix szorozva az egy részvény, vagy mátrix számláló. Ez a módszer lehetővé teszi, hogy a kívánt eredményt anélkül osztály közvetlenül. Ez a cikk leírja, hogyan kell osztani a mátrixban.
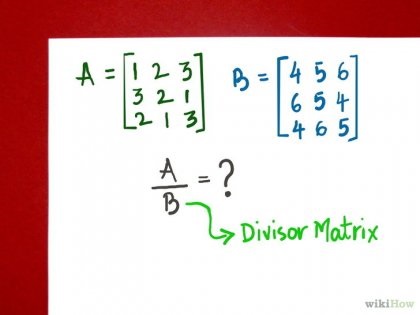
Határozzuk meg a fordított mátrix-nevező. Módszerek megtalálása inverz mátrixok és egyéb műveletek mátrixokkal megtalálható tankönyvek és segédkönyvek a matematika. Számítsuk ki a meghatározója a mátrix-nevező. Az eljárás megtalálásához a meghatározója a mátrix leírt matematikai tankönyvek. E lépés annak meghatározása, hogy a determináns nulla. Ha a mátrix-elválasztó determináns nulla, ez azt jelenti, hogy a mátrix visszafordíthatatlan, azaz nem létezik a fordított mátrixba. Ebben az esetben hagyja abba a további lépéseket. Ha az inverz mátrix-elosztót nem létezik, akkor nem lehet folytatni. Ez a helyzet hasonló a nullával való osztást nem engedélyezett a skalár mennyiségek. Ha a determináns értéke nem nulla, hogy az inverz mátrix-nevező. A leggyakoribb módja a megállapítás a fordított mátrix - módszer Gauss-Jordan és az eljárást a megállapítás a mátrix kofaktoroktól. Ellenőrizze, hogy helyesen talált egy inverz mátrixot. Szorozzuk inverz mátrix az egyenes vonalon, ennek eredményeként van, hogy az identitás mátrix. Az identitás mátrix - ez egy ilyen, amelynek minden eleme nulla, kivéve az átlós, egyenlő egy.
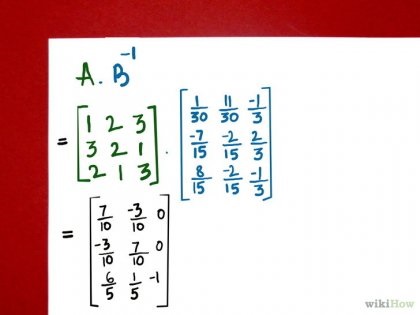
Szorozzuk meg a számláló mátrix-mátrix hátoldalán nevező. Figyeljük meg, hogy, ellentétben a szorzata skalár mennyiségek, ebben az esetben az, hogy a tényezők jelentős. Amikor megszorozzuk számok 2, szorozva 4 azonos eredményt ad, mint a 4 szorozva 2. A vektor-mátrix szorzás matematikai számláló által a nevező fordított mátrix olyan eredményt ad eltérő, hogy ha egy inverz mátrixot megszorozzuk egy mátrix-számlálóban.
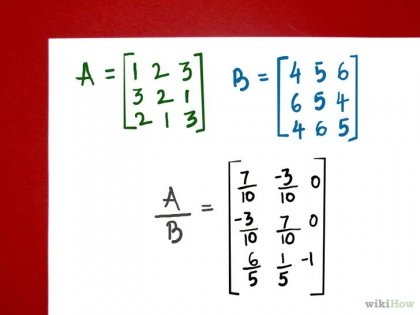
Megjegyezzük, hogy az eredmény szorzata mátrixok között megfelel kívánatos. A mátrix nem szigorúan meghatározott mátrix algebra úgy számítjuk ki, megtalálni a fordított mátrix szorzás és ez osztható mátrix.
254310 254311 254312