A módszer bevezetésének az új változók
A módszer bevezetése egy új változó megoldásában racionális egyenletek egy változót, akkor találkozunk során algebra 8. évfolyam. Ennek lényege, hogy a módszer megoldására egyenletrendszerek ugyanaz, de egy technikai szempontból, vannak olyan jellemzők, amelyek megbeszéljük a következő példák.
3. példa Hogy oldja az egyenletrendszert
Határozat. Bemutatjuk az új változó Aztán az első egyenlet átírható egy egyszerűbb formában: Oldjuk meg ezt az egyenletet a változó t:

Mindkét érték kielégíti a feltételt. és mivel a gyökerek racionális egyenletek változó t. De aztán, olyan, ahol azt látjuk, hogy az x = 2y, vagy
Így a módszer bevezetése egy új változó, mi lett volna képes, mintha „rétegződik” az első egyenletben a rendszer meglehetősen bonyolult megjelenésű, kettővel több, mint az egyszerű egyenlet:
Mi a következő lépés? És akkor mind a két egyszerű levezetett egyenletek viszont meg kell vizsgálni, hogy a rendszer az x 2 - y 2 = 3, ami még nem emlékeztetett. Más szóval, a probléma megoldása csökkenti a rendszer két egyenlet:
Meg kell találni a megoldást az első rendszer, a második rendszer, és minden kapott egy pár értékek közé a választ. Nézzük megoldani az első sor egyenletek:
Az általunk használt módszer a helyettesítés, különösen azért, mert itt minden készen áll rá: 2y behelyettesıtve x a második egyenletben a rendszer. megkapjuk
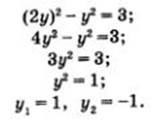
Mivel x = 2y, azt találjuk, rendre x1 = 2, x2 = 2. Így előállított két oldatot adott rendszer (2, 1) és (-2, -1). Mi megoldjuk a második egyenlet:
Ismét használjuk egy helyettesítési módszer: helyettesíti az expressziós 2 y a második egyenletben a rendszer. megkapjuk
Ez az egyenlet nincsenek gyökerei, ezért az egyenletrendszert nincs megoldása. Így a választ kell adni, hogy az csak az első rendszer megoldásokat.
A módszer bevezetésének új változók megoldására rendszer két egyenlet két használt változókat két kiviteli alak. Az első lehetőség egy új változót bevezetni és alkalmazni, csak egy egyenletrendszer. Ez volt a helyzet a példában 3.Vtoroy opció: két új változók bevezetésével és alkalmazásával egyidejűleg mindkét egyenletben a rendszer. Így lesz a helyzet a 4. példában.
4. példa Hogy oldja az egyenletrendszert