Néhány jellemzői körmozgás
A szögsebesség jelöli a görög betű omega (w), ez azt jelzi, a szög, amelynél a test forog egységnyi idő. Ez az érték az ív fokban végigvezetik a szervezet egy ideig. Megjegyezzük, hogy ha a szilárd forog, a szögsebesség a két pont ez a testület állandó lesz. Point közelebb helyezkedik el a forgatás középpontját, vagy több - nem számít, hogy van, Ez nem függ a sugár.
A mértékegység ebben az esetben egy bizonyos fokú másodpercenként, vagy radián másodpercenként. Gyakran a „rad” nem írt, és egyszerűen írjuk -1. Például, azt látjuk, hogy mi a szögsebesség a Földön. A föld miatt a teljes forgatás 360 ° C hőmérsékleten 24 órán át, és ebben az esetben azt mondhatjuk, hogy a szögsebesség egyenlő.
Szintén figyelni a kapcsolatot a szögsebesség és lineáris sebesség:
Meg kell jegyezni, hogy a körkörös mozgás állandó sebességgel - egy speciális esete a mozgás. Azonban a mozgás kerületén egyenetlen. Sebesség változtatható lehet nemcsak irányban, és egyenlő marad abszolút érték, de jelentése változó, azaz a kivéve irányának megváltoztatására is van változás a sebességet a modult. Ebben az esetben beszélünk az úgynevezett gyorsított mozgás egy kört.
Tárgy: törvényei interakció és a mozgás a testek
Lecke 22. problémamegoldás
Eryutkin Eugene S.
A tanulság fordítják problémák megoldása
1. Célkitűzés szentel a egyetemes tömegvonzás törvénye.
Feltételek: határozza meg a magasságot, ahol a gravitációs erő lesz 3-szor kisebb, mint a Föld felszínén.
Adott: SI Megoldás:
h -. Válasz: h »4685 km.
Abban az állapotban, akkor jelezte, hogy a gravitációs erő kell, hogy legyen 3-szor kisebb, mint a Föld felszínén. Az erőssége F1 - a gravitációs erő a test a földre a föld felszínén, és az erő F2 egy bizonyos magasságban.
Mivel a probléma a egyetemes tömegvonzás törvénye. írjuk le a törvényt, de azt kétszer. Az első alkalommal - a szervezet számára, amely található a Föld felszínén, és a második alkalommal - a szervezet számára, ami található egy bizonyos magasságban képest a föld felszínén. Tehát, F1 - ez a gravitációs erő, vagy a gravitációs erő a test, a súlya, amelynek m a földre. A törvény maga írt az alábbiak szerint :.
Most írja a képlet az F2 erő. amely megfelel a kölcsönhatás erőssége közötti kis testtömeg m és a föld, egy bizonyos magasságban a Föld testtömeg H :.
Az ismert állapot, hogy az F1 és F2 köti össze kapcsolatban :. Most összekapcsolják a két egyenletet az egyenletet, és elosztjuk egymással.
Ahhoz, hogy a következő lépés, akkor meg kell, hogy vegye a négyzetgyöke a jobb és a bal oldalon.
Asker kap egy képletet, amely meghatározza a magassága :.
Ha most helyettesíti az összes ismert értékek, megkapjuk a választ: h »4685 km.
Ez a probléma jól jelzi az a körülmény, hogy milyen magasságban tudja elindítani a műhold oly módon, hogy úgy járt el, fajsúlya értékeket. Ez fontos feltétele a tanulmány a mozgás műholdak.
2. feladat szentel egy görbe vonalú mozgás.
Feltételek: kerékpáros mozog a görbület a közúti, az út sugara 50 m, a kerékpáros sebesség 36 km / h. Határozzuk meg a centripetális gyorsulás kerékpáros áramló görbe az út, és határozza meg a súrlódási erő, amely hat a kerék.
Adott: SI Megoldás:
Keresse szükséges AC és a súrlódási erő, amely hat a lovas. Ennek az első 36 km / h lefordítani SI - 10 m / s. Utalva a döntést. Emlékezzünk arra, hogy a centripetális gyorsulás meghatározása az arány a tér a sebesség és a görbületi sugár az út :.
Ebben az esetben tudjuk írni.
Ez a centripetális gyorsulás. Most azt mondhatjuk, ha van egy centripetális gyorsulás, azaz felé kényszeríti az a kör középpontja, akkor jár az ellenzék másik erő -, mert a test mozog egy kört az állandó sugarú csúszás nélkül és csúszik. Ez a súrlódási erő a kerekek között és az út. Ebben az esetben, biztosnak kell lennünk abban, hogy vegye figyelembe, hogy az FTP-Ft. Szerint a Newton második törvénye FTP Ft = = m. AC. Tehát FTP = 60. 2 = H. 120, AC = 2 m / s2 és FTP = 120 H.
Figyeljük meg, hogy ha a súrlódási erő és a centripetális erő nem egyenlő, akkor láttuk volna a csúszás vagy egy forgó kerékpár a kerekítés lenne megtörni az egyensúlyát.
Így megyünk az utolsó, a harmadik probléma, ami kell szentelni a egyenes állásba.
Feltételek: meghatározza egy kezdeti sebessége a test, amely függőlegesen felfelé mozgó, 2 másodperc után a kezdete a mozgás sebességet ért el 5 m / s. Határozza meg a magasság, amelynél a test lesz, ha a sebessége egyenlővé válik 5 m / s.
h -. A válasz: h = 30 m.
Kezdjük egy kezdeti sebességen. Nézd, írunk az első teljes egyenlet alapján. . Emlékezzünk vissza, hogy a gravitációs gyorsulás problémák megoldásában, veszünk egyenlő. Most feltétlenül kell referenciának.
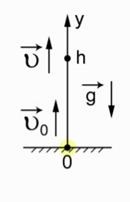
Ábra. 1. A referencia-rendszer választott a probléma megoldására
A referencia képkocka társított a Föld felszínén. Most kompatibilis egyenlet, a sebesség a kiválasztott referencia rendszerrel. Megjegyezzük, hogy az ezzel az referencia-rendszer a kezdeti sebesség irányított függőlegesen felfelé, ugyanabban az irányban, mint az y tengelyen.
Sebesség 2 másodperc, amely úgy definiálható, mint 5 m / s, továbbá függőlegesen felfelé -. Nehézségi gyorsulás irányított függőlegesen lefelé. Itt a nyíl jelzi, már kijelölt ez a gyorsulás. Majd írunk az egyenletet: V = V0 - g. t. Behelyettesítve ismert értékek, van: 5 = V0 - 10. 2.
Ez azt jelenti, hogy a kezdeti sebesség, azaz a a sebességet, amellyel a test öntött függőlegesen felfelé, egyenlő lesz. Így, a sebességi egyenlet és a rendszer a referencia, meghatároztuk a kezdeti sebességét. A következő lépés az a meghatározás, a magasság.
Az egyenlet a mozgás általános formája.
Már mondta, hogy a kezdeti sebességet függőlegesen felfelé, ez lesz egy plusz jel. Gravitációs gyorsulás lefelé irányuló tengelyéhez képest, és egy negatív értéket. Ebben az esetben megkapjuk a magasság, az úthossz egy egyenes vonal mentén - azt. A válasz egyenlő h = 30 m.
A válasz: h = 30 m.