Előadás loci pontok locus (HMT) egy szám
Az előadás a témában: „A pontok helye pontok helye (HMT) egy szám, amely az összes pont megfelelő egy adott tulajdonság, vagy több.” - átirata:
1 pontok helye pontok helye (HMT) egy szám áll, hogy az összes pont kielégíti az előre meghatározott tulajdonság vagy több előre meghatározott tulajdonságokkal. Példák lókuszok kerülete - HMT távoli egy adott pont egy adott távolságot; kör - HMT messze egy adott pont a távolság nem halad meg egy adott.

2 Gyakorlat 1 Kiválasztás pont található a rács csomópontok és távol az O pont olyan távolságban egyenlő 2 (cellaoldalak egyenlő 1). válaszolni:
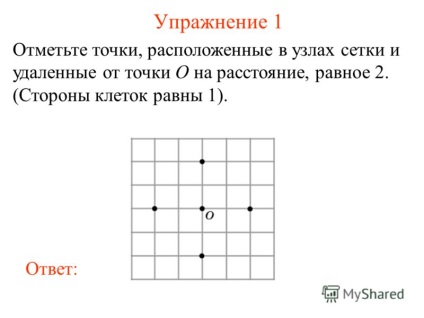
3. megjegyzés 2. gyakorlat pont található a rács csomópontok és távol az O pont által a távolság kisebb, mint a 2. (cellaoldalak egyenlő 1). válaszolni:
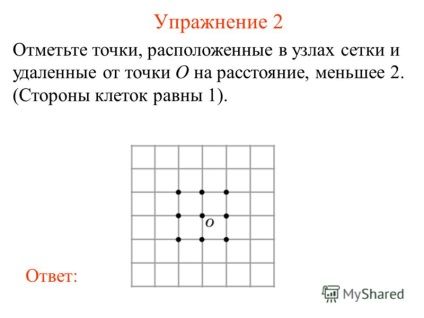
4 3. gyakorlat Kiválasztás pont található a rács csomópontok és távol az O pont nagyobb távolságra, mint 2 és kisebb, mint 3 (cellaoldalak egyenlő 1). válaszolni:
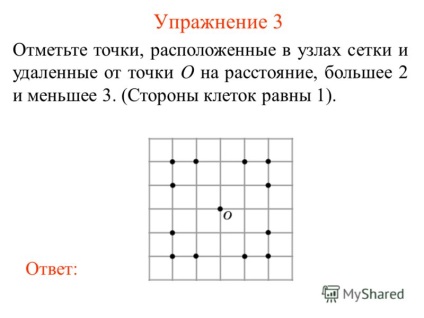
Megjegyzés 4 5 Activity pont található a rácspontok, a távolság, ahonnan az A és B kevesebb, mint három pont. (Felek sejtek 1). válaszolni:
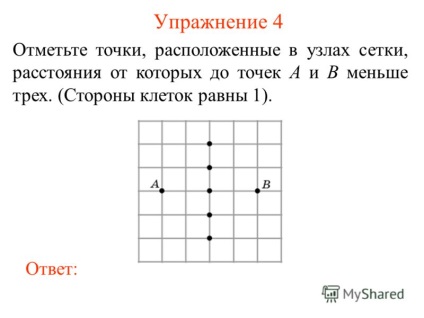
Gyakorlat 5 6 Megjegyzés pont található a rácspontok közötti távolság, amely a pont, A és B kisebb vagy egyenlő, mint kettő. (Felek sejtek 1). válaszolni:
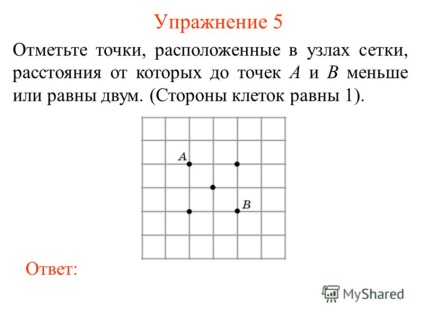
Gyakorlat 6 7 Megjegyzés pont található a rácspontok, amelynek távolsága a pont a kevesebb, mint három, és a távolság a B pont kevesebb, mint kettő. (Felek sejtek 1). válaszolni:
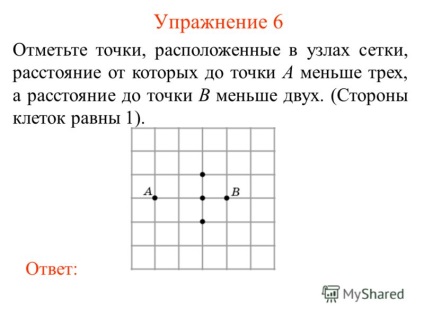
8. gyakorlat 7 Megjegyzés pont található a rácspontok, amelynek távolsága a pont a több mint két és a távolság a B pont kevesebb, mint kettő. (Felek sejtek 1). válaszolni:

9. gyakorlat 8 Megjegyzés pont található rács csomópontok, amelyek távolsága a pont kisebb a távolság, mint a B pont, és a távolság a B pont kisebb, mint a távolság a lényeg C.:

10. gyakorlat 9 Megjegyzés pont található rács csomópontok, amelyek távolsága a pont nagyobb, mint a távolság a B pont, és a távolság a B pont kisebb, mint a távolság a lényeg C.:
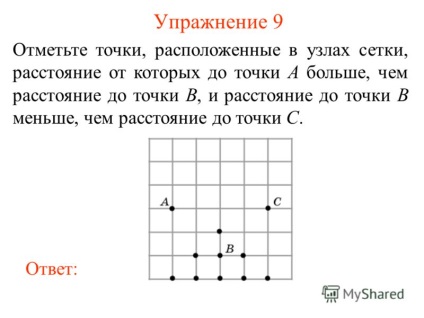
11. gyakorlat 10 Megjegyzés pont található a rácspontok, amelyek a szegmens AB -os szöget zár 90 °. válaszolni:

12. gyakorlat 11 Megjegyzés pont található a rácspontok, amelyek a szegmens AB -os szöget zár 90 °. válaszolni:
Gyakorlat 13 12 Megjegyzés pont található a rácspontok, amelyek a szegmens AB -os szöget zár 90 °. válaszolni:
14. gyakorlat 13 Megjegyzés pont található a rácspontok, amelyek a szegmens AB -os szöget zár 45 °. válaszolni:
15 14. gyakorlat Megjegyzés pont található a rácspontok, amelyek a szegmens AB látható egy 45 ° -os szögben. válaszolni:
16. gyakorlat 15 Megjegyzés pont található a rácspontok, amelyek a szegmens AB -os szöget zár körülbelül 135. válaszolni:
Tétel 17 A középső merőleges. Az egyenesre merőleges szegmens egy lókusz azonos távolságból a végei ebben a szegmensben. Függőleges felezővonal a szegmens az úgynevezett merőleges vonal ebben a szegmensben, és áthalad a közepén. Bizonyítás. Adott egy AB szakasz és D pont - annak közepén. Nyilvánvaló, az O pont egyenlő távolságra pont az A, B és tartozik a függőleges felezővonal. Megfordítva, tegyük fel, hogy a C pont és tartozik a függőleges felezővonal nem esik egybe O, míg a jobb háromszögek a BOC és az AOC (a befogó). Következésképpen, AC = BC. Hagyja, hogy a C pont egyenlő távolságra a A és B pontok, és nem esik egybe a pont O. Ezután a ABC egyenlő szárú háromszög és a CO - medián. By ingatlan egy egyenlő szárú háromszög a medián is magas. Ennélfogva, a C pont tartozik, függőleges felezővonal.
1. feladat 18 Draw locus egyenlő távolságra a pont, A és B:
19 2. gyakorlat A C vonal képet a C pont, egyenlő távolságra pont, A és B:
20 3. gyakorlat Draw locus egyenlő távolságra a pont, A és B:
Gyakorlat 21 4 A vonal c képet a C pont, egyenlő távolságra pont, A és B:
22 5. tevékenység Draw locus egyenlő távolságra a pont, A és B:
Gyakorlat 23 c 6 C vonal képet egyenlő távolságra lévő pont az A és B pontok A:
7. feladat 24 jelölje meg a pontot egyenlő távolságra az A, B és C:
8. gyakorlat 25 jelölje meg a pontot egyenlő távolságra az A, B és C:
9. gyakorlat 26. Jelölje meg a pont egyenlő távolságra az A, B és C:
Gyakorlat 27 10 Döntetlen a locus a központja a körök, amelyek átmennek a két adott pont. A: A merőleges összekötő szakasz két adott pont.
Exercise 28 11 Draw lókusz csúcsú C egyenlő szárú háromszögek egy előre meghatározott bázisszekvencia AB. A: A merőleges AB szegmens nélkül a közepén ebben a szegmensben.
29. 12. gyakorlat Let A és B - a pont a síkon. Adjon locus C-on, ahol a nap AU. Válasz: A fél-sík által meghatározott merőleges a szegmens AB, amely tartalmazza a pont A.
30 Gyakorlat 13 Legyen A és B pontok a síkon, c - egyenes. Adja meg a pontok helye a sorban c, közelebb, mint a B. Ebben az esetben ezeket a pontokat nem kell? A: Része a közvetlen C, amely abban rejlik belül a félig által meghatározott sík merőleges a AB szakaszt, és a pont A. Ha a C vonal rejlik teljesen a félig által meghatározott sík merőleges, és a B pont, akkor nincsenek ilyen pont.
31 szögfelezőtétel. Felezővonal HMT hazudik belül ez a szög, és egyenlő távolságra van az oldalán. Ha a CA = CB, a derékszögű háromszög AOS és VOS (mentén átfogója és egy láb). Ezért, a szögek AOC és BOC egyenlő. Ennélfogva, C felező pont tartozik. Ezzel szemben, ha a C pont tartozik a felezővonal a szög, a derékszögű háromszög AOC és BOC jelentése (a átfogója és hegyesszögben). Következésképpen, AC = BC. Ennélfogva, a C pont egyenlő távolságra levő oldalán a szög. Bizonyítás. Tekintsük csúcsszög C az O pont, és az oldalán egy, b. Hagyja, hogy a C pont fekszik egy adott szögben. Dobd annak CA és CB merőleges az oldalsó és a és b.
1. feladat 32 Draw locus belső szöge AOB pontok egyenlő távolságra az oldalán. válaszolni:
Exercise 33 c 2 Összhangban jelet C pont, egyenlő távolságra a szög AOB oldalán. válaszolni:
34 3. gyakorlat Draw locus belső szöge AOB pontok egyenlő távolságra az oldalán. válaszolni:
Gyakorlat 35 c 4 közvetlen jel C pont, egyenlő távolságra a szög AOB oldalon. válaszolni:
36 5. tevékenység Draw locus belső szöge AOB pontok egyenlő távolságra az oldalán. válaszolni:
Gyakorlat 37 c 6 Az előre jelzés C pont, egyenlő távolságra a szög AOB oldalon. válaszolni:
38 7. feladat Mi a mértani helye központok körök érintő két adott metsző vonalak? Válasz: A szögfelezői által bezárt szögek metszi a adatsort, nincs metszéspontja ezeket a sorokat.
39 8. gyakorlat Válasz: a) A pontokat tartozó négy szögfelezői által bezárt szögek az adatátviteli vonalakon; b) a belső két függőleges által bezárt szögek a szögfelező. Legyenek a és b - metsző vonalak. Find lókusz: a) egyforma távolságra a és b; b) közelebb a, b, mint.
9. gyakorlat 40. A vonal c, metsző oldalán a sarokban, hogy a C pont, egyenlő ezek között oldalon. A: A metszéspontja az egyenest a felezővonal a szög.
Gyakorlat 41 10 Dan AOB és a szög pont M, N a saját oldalán. Belső szög Egy pont egyenlő távolságra van a M és N pontok található és egyenlő távolságra az oldalán a szöget. A: A metszéspontja a merőleges MN a szögfelező.
42 Metszet számok Legyen F 1 és F 2 - számok a gépen. Ábra F álló összes pont tartozó ábra és 1. ábra F F 2, F a kereszteződésekben a számok 1 és F 2 és jelöljük F 1 F 2.
43 1. tevékenység A: A kívánt lókusz a metszéspontja két kört központok pontok O 1, O 2, és a sugarak R 1, R 2 Adott két pont O 1 és O 2 Find lókusz X, 1, ahol R 1 XO és XO 2 R 2. A metszéspontja bármilyen formájú kívánatos lókusz.
44 2. gyakorlat Adott két pont, A és B Keressen egy locus C-on, amely a CA CB AB. A kereszteződés közéleti a kívánt lókusz. Válasz: A kívánt helyre a metszéspontja a kör és a fél-sík.
45 3. gyakorlat Mivel a három pontot az A, B, C. Keresse locus X, amelyre AX BX és BX CX. A kereszteződés közéleti a kívánt lókusz. Válasz: A kívánt lókusz a metszéspontja a két fél-terek által meghatározott középső merőleges szegmens AB és BC.
Kombinálása ábrákon 46 Legyen F 1 és F ábra - 2 a síkban. Ábra F álló összes pont tartozó 1. ábra vagy a kép F F 2 nevezik kombinálásával számok 1 és F 2 és F jelentése F 1 F 2.
Gyakorlat 47 1 Adott két pont O 1 és O 2 Find locus X, 1, ahol R XO 1 vagy 2. R XO 2 Egyesület bármely formában kívánatos helyre. A: A kívánt lókusz az unió két kört központok pontok O 1, O 2, és a sugarak R 1, R 2.
48 2. gyakorlat Mivel a három pontot az A, B, C. Keresse locus X, amelyre AX BX és BX CX. Egyesület közéleti kívánt helyre. Válasz: A kívánt lókusz az unió két fél-terek által meghatározott középső merőleges szegmens AB és BC.
A különbség a számok 49 Legyen F 1 és F ábra - 2 a síkban. Ábra F álló összes pont tartozó ábrán F 1 és F 2 tartozó szám, az úgynevezett a különbség a számok 1 és F 2 és F 1 jelentése F \ F 2.
50 1. tevékenység A: A kívánt lókusz a különbség a két kört központok pontok O 1, O 2, és a sugarak R 1, R 2 Adott két pont O 1 és O 2 Find lókusz X, 1, ahol R 1 XO és XO 2 R 2. A különbség a formák, amelyek kívánatos lókusz.