tulajdonságok eltérés
Funkciók: \ (f \) \ (u \) \ (v \)
Az érvelés (független változó): \ (x \)
A differenciálhányados: \ (y '\ left (x \ right) \), \ (f' \ left (x \ right) \)
Constant: \ (C \)
Tényleges szám: \ (A \) \ (\ alpha \)
Növelés funkció: \ (\ Delta y \)
A növekmény a független változó: \ (\ Delta x \)
Eltérés funkció: \ (dy \)
A differenciál a független változó: \ (dx \)
Tekintsük az \ (y = f \ left (x \ jobbra) \), és feltételezik, hogy egy bizonyos ponton \ (x \) argumentum növekszik \ (dx \), amely az úgynevezett differenciális a független változó. A funkció \ (y = f \ left (x \ right) \) olyan differenciál a ponton \ (x \), ha annak növekmény leírható összegeként két kifejezés:
\ (\ Delta y = f \ left (\ jobbra) - f \ left (x \ right) = A \ Delta x + \ alpha, \)
ahol az együttható \ (A \) nem függ \ (\ Delta x \), és az értéke \ (\ alpha \) van egy magasabb rendű kicsinység lépésekben \ (\ Delta x \), azaz a \ (\ alpha / \ Delta x \ 0 \), ha a \ (\ Delta x \ 0 \).
A rögzített képlet fő lineáris része a növekmény az úgynevezett differenciális függvény \ (f \ left (x \ right) \) azon a ponton, \ (x \), és jelöli, \ (dy = A \ Delta x \). Ebben a kifejezésben, az együttható \ (A \) az az érték, a származtatott \ (f „\ left (x \ right) \) azon a ponton, \ (x \).
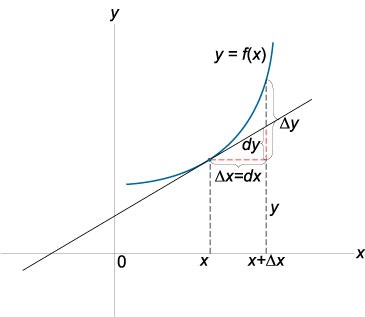
Differenciál független változó megegyezik annak növekmény:
\ (Dx = \ Delta x \)
A differenciál funkciója megegyezik a terméket a származék a differenciális a független változó:
\ (Dy = df \ bal (x \ right) = f „\ left (x \ right) dx \)
Expression keresztül származékot differenciálművek
\ (F „\ left (x \ right) = \ nagy \ frac >> \ normalsize \)
Differenciál állandó számot nullával egyenlő:
\ (DC = 0 \)
Eltérés az összege funkciók az összege a különbségek:
\ (D \ bal (\ right) = du + dv \)
Eltérés különbség funkció a különbség különbségek:
\ (D \ left (\ right) = du - DV \)
A konstans tényező lehet venni, mint egy jel a különbség:
\ (D \ bal (\ right) = CDU \)
Eltérés a termék a funkciók
\ (D \ bal (\ right) = VDU + UDV \)