Turing-gép
A művészi ábrázolása a Turing-gép
Turing-gép (TM) - absztrakt művész (elméleti számítógép). Alan Turing ajánlottak 1936 hivatalossá fogalma algoritmus.
Turing-gép egy kiterjesztése egy véges automatát, és a szerint Church tézise - Turing. képes szimulálni előadók (azáltal átmeneti szabályok) semmilyen módon megvalósító számítási lépés eljárás, amelyben minden egyes lépés kellően elemi számítás.
Azaz, minden intuitív algoritmus lehet megvalósítani olyan Turing-gép [1].
A készülék a Turing-gép [szerkesztés | szerkesztés wiki szöveg]
A kompozíció a Turing-gép tartalmazza mindkét oldalán kötetlen szalagot (lehetséges Turing gépek, amelyek több végtelenített heveder), osztva a sejteket [2] [3]. és a vezérlőegység (más néven író-olvasó fej (GZCH)), hogy lehet az egyik a több államban. A számos lehetséges vezérlő egység állapotok véges, és pontosan meghatározott.
A vezérlő eszköz úgy működik, a szabályok szerint az átmenet. amely egy algoritmus által végrehajtott ezen Turing-gép. Minden átmeneti szabály előírja, hogy a gép, attól függően, hogy a jelenlegi állapot és a megfigyelt az aktuális karaktert sejtet, hogy írjon a cellába egy új szimbólum, menjünk át egy új állam, és mozgassa az egyik cellából a balra vagy jobbra. Egyes állami Turing-gép lehet címkézni egy terminál. és az átmeneti ezek közül bármelyik végét jelenti a munka, megáll az algoritmus.
A Turing-gép az úgynevezett determinisztikus. Ha minden kombinációja államok és szimbólumok a szalagot táblában lévő legfeljebb egy szabályt. Ha van egy pár „ribbon szimbóluma - állam”, amelynek van 2 vagy több csapat, úgynevezett nem-determinisztikus Turing-gép.
Leírás Turing-gép [szerkesztés | szerkesztés wiki szöveg]
Konkrét Turing-gép van beállítva felsorolja az ábécé meg az elemek egy, a beállított Q államok és egy sor szabályt, amellyel a gép működik. Ezek formájában :. Qi aj → qi1 Aj1 dk (ha a fej az állam qi és a megfigyelt sejt írott levelében aj a fej mozog az állami qi1 cella helyett AJ rögzített Aj1 fej teszi mozgás dk, amelynek három lehetőség ....: a cella a bal (L), egy sejt, hogy a jobb (R), hogy a helyén maradjon (N)). Minden lehetséges konfiguráció,
Egy példa a Turing-gép [szerkesztés | szerkesztés wiki szöveg]
Itt egy példa MT megszorozzuk számok unáris jelölést. Vedd szabályok «qi aj → qi1 Aj1 R / L / N» kell érteni: qi - olyan állapot, amelyben ez a szabály teljesül, aj - az adatokat a cella, amely a fej, qi1 - az állam, amelyben meg kell, hogy menjen, Aj1 - meg kell írva a sejtben, R / L / N - Mozgatás parancsot.
A gép az alábbi szabályok:
terminális állapotban (stop algoritmus)
Szorzás alkalmazásával 2 MT 3 egy rendszerben. A megadott protokoll kezdeti és végső Államok MT, a kezdeti konfiguráció a szalagot, és a helyét a gép feje (aláhúzott karakter).
Kezdeni. Mi állapotban vannak a q0. Beléptünk a gép adatok: * 111x11 = *, akkor a készülék feje van elhelyezve az első karakter *.
1. lépés. Nézzük a szabálytáblázatok, hogy majd az autót, amíg az állam q0 felett a „*” jelet. Ez a szabály az 1. oszlopban az 5. sor - q0 * → q0 * R. Ez azt jelenti, hogy haladunk az állam a q0 (azaz nem változnak meg), a jel lesz „*” (azaz, nincs változás), és van feszítve «* 111x11 = *» jobbra egy pozícióval (R) már beírt szöveget, azaz az 1. szimbólum 1. feldolgozott szabály q0 1 q0 → 1R Cserébe az állam q0 1 (1. oszlop 1. sor). Azaz, megint, ott is csak egy átmenet a 1 pozícióval jobbra. Ez akkor történik, amíg nem fogunk az „x” jellel. És így tovább: hogy az állami (indexen q), hogy a karakter a standon (aláhúzott karakter), és csatlakoztassa őket nézni feldolgozására kapott kombináció szabály táblázatban.
Egyszerűbben fogalmazva, a szorzás algoritmus: bejelöljük az 1. egység 2. faktor, helyette a „a” betű, és húzza az egész 1. tényező az egyenlőségjel. Az átcsoportosítás történik felváltva cseréje egységek 1. szorzó „a” és mellékelik az egységek száma a sor végére (a bal oldalon a jobb szélső „*”). Akkor változik az összes „a” a szorzás jele „x” vissza a készüléket. És a ciklus ismétlődik. Sőt, mivel A szorozva B úgy reprezentálható, mint A + A + A időben. Most címke a 2. egység 2. faktor az „a” betű és újra át a készüléket. Amikor a „=” jel nem jelenik egységek - így a szorzás befejeződött.
Turing teljesség [szerkesztés | szerkesztés wiki szöveg]
Azt mondhatjuk, hogy a Turing-gép egy egyszerű számítási gép lineáris memória, amely szerint a formai szabályok alakítja a bemenő adatokat egy sorozata atomi lépéseket.
Elementary intézkedések, hogy a változtatások hatását csak egy kis adat a memóriában (abban az esetben a Turing-gép - csak egy cella), és a számos lehetséges intézkedések természetesen. Annak ellenére, hogy az egyszerűség a Turing-gép, akkor lehet számítani, amit ki lehet számítani minden más gép, számítások elvégzése elemi akciójelenetek. Ezt a tulajdonságot nevezzük teljességében.
Az egyik természetes módon bizonyítani, hogy a számítási algoritmusok lehet végrehajtani egy gépen lehet megvalósítani, és a másik - ez egy utánzat az első gép a második.
Mint már említettük, a Turing-gép képes szimulálni (beállításával átmeneti szabályok szerint) az összes többi fellépő bármilyen módon megvalósító számítási lépés eljárás, amelyben minden egyes lépés kellően elemi számítás.
Egy Turing-gép képes szimulálni a gép nagyböjt. Markov normál algoritmusok és bármilyen hagyományos számítógépekre szánt szoftvereket, átalakítja vizekbe való kimenet bármely algoritmus. Az viszont, különböző absztrakt művészek lehet szimulálni Turing-gép. Művészek, amelyekre ez lehetséges, az úgynevezett teljes Turing (Turing-teljes).
Van hagyományos számítógépekre szánt szoftvereket, amelyek utánozzák a munka egy Turing-gép. De meg kell jegyezni, hogy a szimuláció nem teljes, mivel van egy Turing-gép absztrakt végtelenített szalag. Végtelenített szalag az adatokat lehetetlen teljesen szimulálják a számítógép véges memória (összesen számítógép memóriájában - RAM, merevlemez, a különböző külső adathordozóra, regiszterek, és a CPU cache, stb -. Legyen nagyon nagy, de mégis, mindig természetesen).
Változatok Turing-gépek [szerkesztés | szerkesztés wiki szöveg]
A modell egy Turing-gép bővíthető. Egy figyelembe lehet venni egy Turing-gép egy tetszőleges számú szalagok és többdimenziós szalagok különböző korlátozásokat. Azonban minden ilyen gépek teljes Turing és szimulált hagyományos Turing-gép.
Turing-gép dolgozik egy félig végtelen szalag [szerkesztés | szerkesztés wiki szöveg]
Egy példa az ilyen információt, úgy az alábbi tétel: Egy Turing-gép van egy egyenértékű Turing-gép működő félig végtelen szalagot (azaz a szalag, a végtelen egyirányú).
Tekintsük a bizonyíték, öntött G. Karpov könyvében „Automata Theory”. A bizonyítás konstruktív, azaz megadunk egy algoritmust, amellyel bármely Turing-gép egyenértékű a Turing-gép egy bejelentett ingatlan építhető. Először is felsorolni tetszőleges üzemi szalag MT sejt, azaz meg egy új helyen, a szalag információk:
Ezután felsorolni sejtek sőt, azt feltételezzük, hogy a „*” jel nem szerepel a szótárban MT:
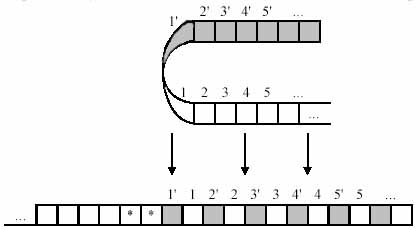
Végül, változtassa meg a Turing-gép, megduplázva a száma annak államok, és a változás a váltás író-olvasó fej úgy, hogy az egyik csoport a gép állapotát egyenértékű lenne munkáját az árnyékolt terület, míg a másik csoport az állam gép fog működni, mint az eredeti gép működik az árnyékolt terület. Ha az MT találkozik a karakter „*”, akkor az író-olvasó fej elérte a határ közelében
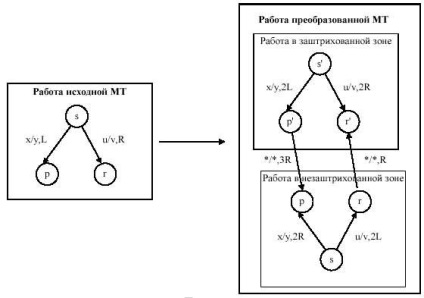
A kezdeti állapotban az új Turing-gép van telepítve egyik vagy másik terület attól függően, milyen része az eredeti szalag helyezkedik postakönyvét az eredeti alakját. Nyilvánvaló, hogy a bal oldalon a korlátozó markerek „*” ekvivalens Turing-gép nincs használatban.
Kétdimenziós Turing-gép [szerkesztés | szerkesztés wiki szöveg]
. Lásd még [szerkesztés | szerkesztés wiki szöveg]
Más előadók absztrakt és formális számítás rendszerek [szerkesztés | szerkesztés wiki szöveg]
Megjegyzések [szerkesztés | szerkesztés wiki szöveg]
3. Az állam gép - véges állapotú gép vagy véges állapotú automata, véges automata, vagy egyszerűen egy olyan gép, egy matematikai számítási modell. Ez a gép, amely lehet pontosan egy olyan véges sok állapot bármikor. Az FSM lehet változtatni az egyik állapotból a másikba válaszul a külső bemenetek. A FSM határozza meg listája államok, az állapota. A gépek viselkedését is megfigyelhető sok eszköz a modern társadalomban, hogy végre egy előre meghatározott sorrendben cselekvések függően az események sorozatát, amellyel bemutatják. A véges állapotú gép kevesebb energiát, mint más modellek számítási, mint a Turing-gép. A számítási teljesítmény különbséget jelenti vannak olyan feladatok, hogy a Turing-gép tehet. Ez azért van, mert a ÉBIR memória korlátozza az államok száma azt, ÉBIR tanulmányozták az általánosabb területén automaták elmélete. Egy példa a mechanizmus, amely lehet modellezni egy gép egy beléptető kapu. A beléptető kapu, használt hozzáférés aluljárók és vidámpark túrák, egy kapu három forgó fegyverek derék magasságban, egy egész bejárat. Kezdetben a karok vannak zárva, blokkolja a belépési, megakadályozva előfizetett áthaladását, letétbe egy érme vagy token egy slot a beléptető kapu feloldja a karok, amely lehetővé teszi egy ügyfél, hogy álljon át. Miután az ügyfél áthalad, a karok vannak zárva, amíg a másik érme bedobását, úgy mint állam gép, a beléptető kapu két lehetséges állapot nyitását és zárását. Két bemenet, ez befolyásolja az állam, amivel egy érmét a nyílásba, és nyomja a karját. A lezárt állapotban nyomja a kar nincs hatással, nem számít, hogy hányszor bemeneti nyomja meg van adva, amivel egy érme - azaz, így a gép egy érme bemenet - eltolódik az állam Zárt hogy kártyafüggetlen. A nyitott állapotban van, ami további érmék nincs hatással, azonban az ügyfél nyomja át a fegyvert, ami egy push bemenet, az eltolódások az állam vissza Lezárt. Mindegyik állapotot képviseli egy csomópont, élek mutatják átmenet egyik állapotból a másikba. Mindegyik nyíl van feltüntetve a bemeneti kiváltó hogy átmeneti, egy bemeneti amit nem okoz változást az állami képviseli egy körkörös nyíl visszatér az eredeti állapotába. A nyíl a Locked csomópontot a pont jelzi, hogy a kiinduló állapot