Mágikus polyhedra

Nyilvánvaló, hogy nincs határ kombinatorikus problémák, ami kell a címkén élek, csúcsok vagy arcok különböző poliéderek így kapott mágikus konstans, a váratlan módon. Sok ilyen feladatok alakíthatók egyenértékű probléma mágikus csillagok. Például ez. Melyik az öt jogok

il geometriai testek varázsolni, miután jelölt szélük úgy, hogy a számok összege a csúcsok ugyanaz volt? És meg kell tenni még egy feltétel - a szám nem lehet egy sorszám. Könnyen belátható, hogy ez nem a tetraéder. Ez lehet olvasni a könyvben a hatodik könyve Mathematical Games a Scientific American ( «a hatodik könyv a matematikai játékokat Scientific American magazin"). Lehet, hogy ez egy kocka? Egy kocka 12 szegélyei (lásd. Ábra bal). Megjegyzés: a 12 fekete pontok a csúcsai octagram (jobbra). Mivel minden egyes tesztelt pont két vonal legyen egyenlő állandó (2h78) / 8, vagy 19.5.

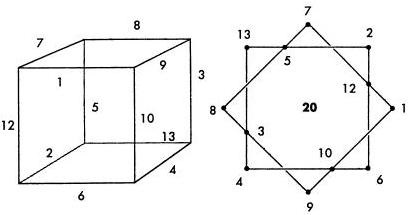
Ez a szám nem egész, ezért nem szükséges keresni a választ. Ugyanakkor tudjuk, hogy egy hibás döntés (nem felel meg az utolsó feltétel) a legkevésbé mágikus konstans 20, és a legkisebb maximális száma 13 jelölt körök (és az azzal egyenértékű széleit a kocka), ahogy az ábrán látható.

Mivel az oktaéder duális a kocka, azt eredményezi, hogy az automatikus megoldást a problémára a széleit az oktaéder címkézés különböző ellentmondásos nullától pozitív egész szám, amelyek összege körül minden arc ad a mágikus állandó, és a legkisebb.

Mint láttuk, a szélei oktaéder megjelölheti a egymást követő egész szám oly módon, hogy a felső acél varázslat. Az ikozaéder és a dodekaéder magic constant frakcionált fordulat, úgy, hogy nem lehet egy megoldás a problémára. Mivel minden poliéder kettős pár, köztük egy, amely eleget tesz a feltételeknek hasonló problémák (teljes, nem nulla sorszám, de mágikus arcok) nem létezik.

Kapcsolódó tartalom:

Oszd meg barátaiddal:

Vizsgálatok:

Term papírok:

Kapcsolódó cikkek

• Ametiszt kő - gyógyító és mágikus ékszer ametiszt

• Attack mágikus gömb hideg - aion tudásbázis

• 78 Magic Circle