Funkciók használata tárca, MDETERM és MMULT
1. Keresse meg a fordítottja:
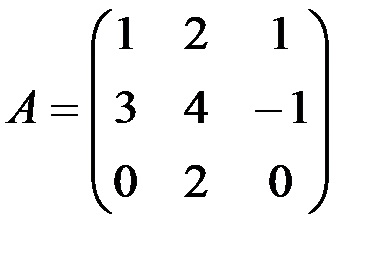
· Írja be a mátrix elemei a tartományban az A1: C3;
· Ahhoz, hogy a fordított mátrixba nem függő válasszon egy sor sejtek az azonos méretű, például E1: G3, és adja meg a tömbképletet. A következtetés az formula zárójelek megadása után a képlet, nyomja meg a CTRL + Shift + Enter.
2. Számítsuk ki a meghatározója a mátrix A. Ehhez válasszon egy használaton kívüli sejt, azaz például A5, és adja meg a képlet
3. Számítsuk ki a terméket a mátrix, a mátrix-B, ahol
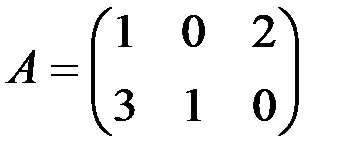
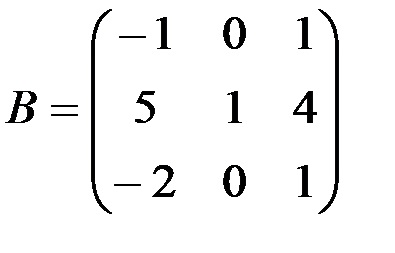
· Írja be a mátrix elemei egy tartományban sejtek A10: C11;
· Írja be a mátrix elemei egy sor sejtek a A13: C15;
· Kiválasztása cellatartományt az azonos számú sort, mint a tömb A. és az azonos számú oszlopok egy tömbben. így például, E10: G11 és írja be a képletet
4. Problémák a rendszer lineáris egyenletek 3 ismeretlenek
fordított mátrix által.
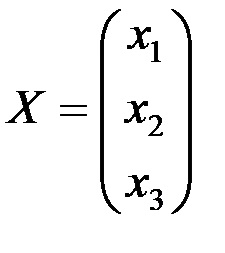
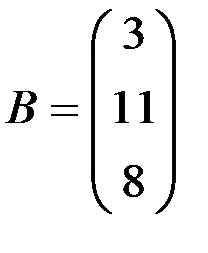
Az oldatot (1) mátrix formában van formájában AX = B,
ahol: A - az együttható mátrix;
X - oszlop ismeretlen;
B - oszlop szabad kifejezések.
Feltéve, hogy egy négyzetes mátrix (2) (1) a nem-degenerált, azaz determinánsa | A | ¹ 0, egy inverz mátrixot rendszer A. Ezután az oldatot a fordított mátrix módszer oszlopmátrix X = A B. Mi találni ezt a megoldást. Ehhez:
· Mi található a meghatározó | A | = 5 (lásd ábra. F. 2.). Ahhoz, hogy aktiválja ezt az új munkalapot, és bevezetni az együtthatók a mátrix elemek egy sor sejtek A1: C3. Isolate bármelyik szabad helyzetben, például a A5, és bevezetni a képlet
· Mivel | A | ¹ 0, akkor A - nem szinguláris és van egy inverz mátrixot Analyzed fordított mátrixba. Ehhez válasszon ki egy nem érintkező tartományban sejtek az azonos méretű, mint a mátrix A. pl E1: G3, és adja meg a tömbképletet.
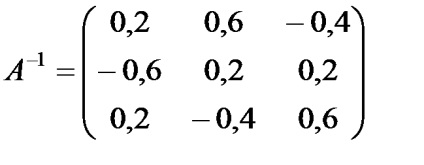
· Mi megtalálja a megoldást a rendszer az oszlop formájában mátrix
X = A B .. Ehhez bevezetjük a mátrix elemei egy cellatartományba E6: E8, válasszon ki egy cellatartományt az azonos számú sort, mint a tömb A. és az azonos számú oszlopok egy tömbben. így például, G6: G8 és bevezetni tömbképletet
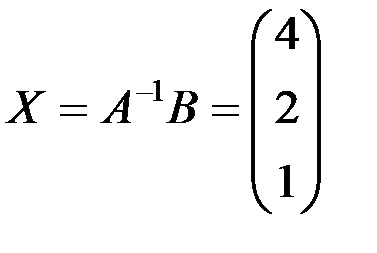
azaz oldatot a rendszer (4, 2, 1).