Momentum és energiát a speciális relativitáselmélet
Momentum és energiát a speciális relativitáselmélet:
A relativisztikus mechanika tivistic törvénye lendületmegmaradás: bármely folyamat, hogy egy zárt rendszerben, a lendület (.. Azaz a geometriai összege a termékeket a relativisztikus tömeg minden alkatrész a rendszer a saját sebesség) nem változott etsya. Az alapvető egyenlet relativisztikus di Namiki a formája
- Test impulzus (anyagi pont) a relativisztikus mehanike.Mozhno mutatják, hogy egyenlet (7,21) kielégíti Lorentz invariancia, ha az átmenet az egyik inerciális referencia rendszert átalakítani a másik erőkomponensek a tengelyek mentén a törvény által meghatározott. Alacsony sebességnél (<<с) масса те-ла mm0 =const и релятивистское уравне-ние (7.21) совпадает с основным законом ньютоновской динамики (2.5), а импульс тела является линейной функцией его скорости: p=m0 v=mv. У всех тел масса покоя m0>0. Ezért, amint azt a képletekben (7,20) és a (7.22), a relativisztikus tömeg és lendületet kell növelni a végtelenségig hajlamos test sebessége a fénysebesség vákuumban. Minden valós teljesítmény véges méretűek, és ezek hatását a szervezetben a korlátozott szám. Nem tudják megmondani a test végtelenül nagy lendületet. Következésképpen a test sebessége képest Bármely inerciális vonatkoztatási rendszer nem lehet egyenlő a fény sebessége vákuumban, és mindig kisebb, mint azt. Ez igaz is atomok, molekulák, és az összes elemi részecskék, kivéve fotonok. Találunk egy kifejezés a kinetikus energia egy részecske relativisztikus mechanika-CIÓ. A növekmény a kinetikus energia egy anyagi pont az elemi elmozdulás dr Mr. egyenlő munkáért Sauveur-kiküszöbölése ebben mozgató ereje az F alapján eljárva anyagi pont:
ahol v pont sebességét. Ha változik a sebesség az anyag pontos lépésekben kinetikus-cal energia és relativisztikus tömeg pro-arányos egymással:
A kinetikus energia, helyhez kötött pont-Ki ( = 0) nulla, és ez a relativisztikus tömeg m0. Ezért, integráló az egyenlet (7,24) az m-re a m0 m, félig-jelöli a következő kifejezés a kinetikus energia a XYZ anyagi pont:
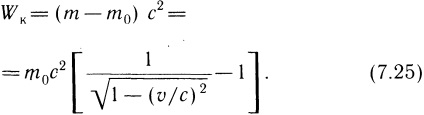
Az általunk használt Taylor bővítése:
E
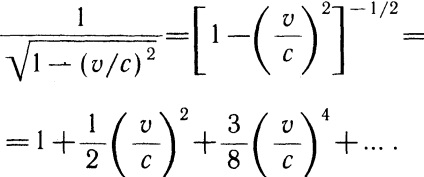
Így, alacsony sebességgel a részecske mozgás mozgási energiájának számított XYZ relativisztikus képletű (7,25) egybeesik az értéke ennek az energiának-em a newtoni mechanika. Azonban nagy sebességek kép sósav-pont mozgási energiájának Wc = (m-m0) 2, és eltér m0 2/2, és az M0 2/2. Képletek (7,24) és a (7,25) érvényes, is van egy rendszer pont (például egy szilárd anyag), mozgó darabban a v sebességgel.