A tanulmány a módszerek megoldására rendszer differenciálegyenletek állandó mátrix
2. Nyilatkozat a probléma
6. Építési általános döntési mátrix módszer
7. A Cauchy probléma a mátrix módszer
Tekintsünk egy rendszert elsőrendű lineáris egyenletek írva az általános formában:
ahol Aij együtthatók. i = 1,2, .... N, a = 1,2, ..., n, pedig állandók;
yi = yi (t), i = 1,2, ..., n - ismeretlen függvények a t változó.
Ha minden bi (t) (i = 1,2, ..., n) értékét nullára (bi (t) = 0), akkor egy homogén szerinti rendszer inhomogén rendszer (1).
Jelölő mátrix rendszer által a (x) és a vektor
akkor a rendszer (1) átírható mátrix formában
, akkor megkapjuk a megfelelő rendszer homogén egyenlet
Bármely sor n funkciók
definiált és folyamatosan differenciálható az intervallumban (a; b), az úgynevezett oldatot (1) ebben a tartományban, ha felhívja az összes egyenletet a (1) az identitás:
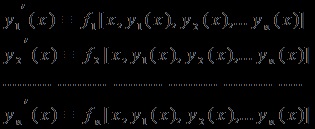
érvényes minden x értékei intervallumban (a, b). Az általános megoldás az inhomogén rendszer az összege az oldat teljes a megfelelő homogén rendszerrel és saját inhomogén megoldásokat.
2. Nyilatkozat a probléma
Célkitűzés: A vizsgálati módszerek megoldani egy differenciálegyenlet-rendszert állandó mátrix:
;
;
1. Keresse meg a sajátértékek és épít az alapvető rendszer megoldások (FSS).
2. Készítsen egy alapvető mátrix az Euler módszer.
3. megtaláljunk egy hozzávetőleges megoldást formájában egy mátrix sor.
4. építsünk egy közös megoldás mátrix módszer. Vizsgálni a függőség a Jordán forma A mátrix saját számokat.
5. Oldja meg a Cauchy probléma.
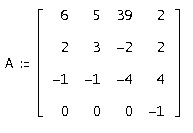
A vektor kezdeti feltételek: [1, 2, 3, 4]
A homogén lineáris differenciálegyenlet-rendszert egy egyenletrendszer a következő formában:
Ha a rendszer mátrix
= Const, akkor a rendszer az úgynevezett rendszer állandó együtthatós, vagy állandó mátrix.
Az alapvető rendszer a homogén lineáris egyenletrendszer az úgynevezett alap megoldások egy lineáris tér a megoldások egy, azaz n lineárisan független megoldásokat a rendszer.
A konstrukció alapvető rendszer megoldások differenciálegyenletek szükséges megtalálni a sajátértékek a karakterisztikus polinom, hiszen attól függően, hogy típusa (jellemző számok igen különböző lehet, több, komplex) beépített alapvető rendszer megoldásokat.
Annak érdekében, hogy ez a rendszer a n lineáris homogén egyenlet n ismeretlennel van nemtriviális megoldás, szükséges és elégséges, hogy a determináns (Wronskian) volt egyenlő nullával:
Ebből az egyenletből fokú n által meghatározott k érték, ahol a rendszer nem-triviális megoldásokat. (4) egyenlet az úgynevezett jellemző.
Írunk a karakterisztikus polinom erre használjuk a funkciót CHARPOLY
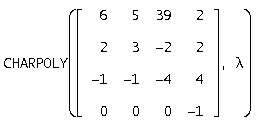
Ahhoz, hogy megtalálja a sajátértékek használata funkciót SOLVE (U, L), amely visszatér a sajátértékei A mátrix a vektorba l. kapjuk:
Ez van két valós gyöke
és két komplex konjugált gyökerek
. Következésképpen, a vektor képező alapvető mátrixot a gyökerek az ilyen típusú lesz külön
. Írunk a DCF adatokat kapott jellemző értékek:
Mátrix y (x), amelynek oszlopait a megoldások képező alapvető rendszert nevezzük alapvető mátrix.
És az általános megoldás a rendszer a következő lesz:
Keressük a megoldást, hogy ezt a rendszert használja Euler módszer.
Euler módszer a következő.
Megoldás A rendszer (1) formájában van kialakítva:
Funkció (5) egy olyan oldat rendszer (1) ha a
- sajátértéke A, és A - sajátvektorának ennek a mátrixnak számának megfelelő
. Ha a sajátértékek
n mátrix eltérő és a1. a2. ..., egy megfelelő sajátvektorai ez a mátrix, az általános megoldás (1) egyenlet által meghatározott:
Abban az esetben, több gyökerei a megoldás a rendszer formájában
ahol Pi (x) polinomok foka nem nagyobb, mint (k-1), amelynek több együttható k tetszőleges. Tehát között együtthatóit ezen polinomok a együtthatók önkényes, és a maradék a · n-k vannak kifejezve rajtuk keresztül. Ahhoz, hogy megtalálja a polinom együtthatóit a helyettesítő megoldás (6) az eredeti egyenletrendszer egyenlővé együtthatók ugyanazokat a funkciókat. Megoldjuk a rendszer tekintetében a (k · n-k) együtthatók. Kapunk egy kifejezés minden együttható keresztül ingyen.
Ha több sajátérték
A annyi lineárisan független sajátvektor
, annak multiplicitás, akkor felel meg k független megoldások az eredeti rendszer:
Ha saját értékeit
multiplicitás k már csak m (m , megtalálható formájában a termék a polinom foka k - m Ahhoz, hogy megtalálja a vektorok , meg kell helyettesíteni az expressziós (4) a (3). Egyenlővé együtthatók hasonló kifejezések a bal és jobb oldalán a rendszer, megkapjuk az egyenlet a vektor . Erre a feladatra a következő sajátérték talált: . Mi épül alapvető rendszer megoldások: Talált 1 sor alapvető mátrixa megoldások a jellemző számok . Írunk a harmadik sorban a döntések általánosságban:
Aij ahol megtaláljuk a kifejezést:
Exponent e A mátrix összege a sorozat
ahol E - az identitás mátrix.
A tulajdonság a mátrix exponenciális:
a) ha AB = BA, azaz A + B = E A + E B = e A + E B;
b) ha A = S - 1 * B * S, azaz A = S -1 * e B * S, ahol a mátrix S - egy transzformációs mátrix a változók eigenbasis alapján az eredeti változók.
c) mátrix y (t) = e A a döntési mátrix Cauchy-probléma:
azaz az alapvető mátrix rendszer (1).
Tól tulajdonságok), ebből következik, hogy az oldatot az y (t) a rendszer (1) megfelel annak a feltételnek a y (0) = y0. által meghatározott expressziós y (t) = e A * y0. Így a probléma a megoldásokat találjanak a egyenletrendszer (1) egyenértékű a probléma megtalálni a mátrix e A mátrix
Kiszámításához a mátrix e At kényelmes, hogy képviselje a mátrix formájában:
,
ahol a mátrix S - egy transzformációs mátrix a változók eigenbasis alapján az eredeti változók, és a BA - Jordan formában mátrix, például a e A = S -1 * e Bt * S.
Jordan forma mátrix függ, hogy milyen jellemző számokat.
1. Tegyük fel, hogy a jellemző értékei a tényleges szeres, míg Jordan formájában dimenzió NxN mátrix a forma:
- valódi gyökér multiplicitás n.
2. Ha a gyökerek a karakterisztikus polinom olyan, mint valóban eltérő, és valódi többszörös gyökerek, a mátrix a következő formában:
- tényleg más gyökerek és
- valódi gyökere sokaságának 2.
3. Ha a gyökerek komplex konjugált gyökkel A Jordán sejt karakterisztikus polinomja a következő:
komplex konjugáltját gyökér a karakterisztikus polinom.
Mivel ebben az esetben többek között az jellemző értékek vannak jelen, mint egy komplex konjugált gyökerek n = 2 - # 59329; ∨ L = 2 + # 59329;, és érvényes a különböző gyökerek L = -1 ∨ L = 1, akkor a Jordan mátrix a következő:
A következő egyenletből S = A * S * V, ahol S - a nem-szinguláris mátrix, kapunk egy rendszert a 16. sorrendben, ahonnan találunk a mátrix elemeinek S. A kapott S mátrix a következő:
Megoldása a rendszer a 16.-sorrendben a következő egyenletből: A * S = S * B

Mi újra néhány elem és így a következő mátrix S:
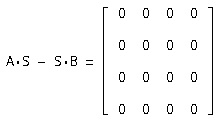
Így az átmeneti mátrix talált igaz.
Megoldásokat találni y vektor kell megszorozni a S mátrix
- egy vektor, amelynek elemei függ a gyökerek a karakterisztikus polinom:
Komplex számok
Ez a következő:
Abban az esetben, valódi gyökereit más:
=
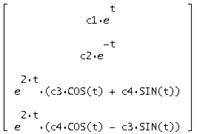
Ezért tapasztaljuk, hogy az általános megoldást y = S *
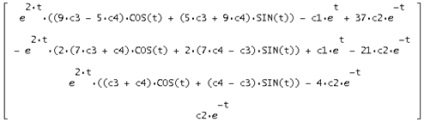
Ha ebben az esetben a megoldás az eredeti rendszert kapunk valódi egyenlőség, ebből következik, hogy a talált megoldás igaz:
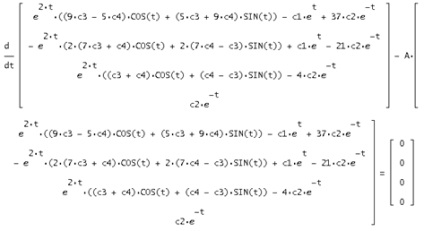
7. A Cauchy probléma a mátrix módszer
Szükség van minden oldatok egyenletek megoldást találni, amelyben Y (i) (t) kap egy előre meghatározott számérték y0i egy előre meghatározott ponton, azaz ci találni értékeket a következő adott értékek: x = 0, y = [1, 2, 3,4].
A vektor a döntések y (t) helyettesítő előre meghatározott körülmények között, és oldja a kapott rendszer a C1, C2, C3, C4:
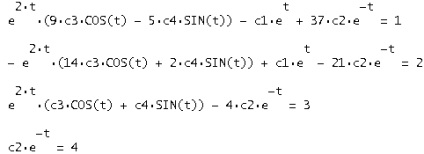
Az eredmény:
Ha ebben az esetben a C1, C2, C3, c4v általános megoldás jutunk oldat formájában Cauchy:
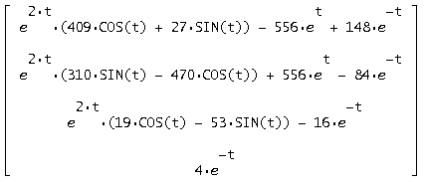
:

Az eredmény egy nulla vektor
. Következésképpen, az oldatot által talált a mátrix az eredeti rendszer.
Let J - Jordan blokk mátrix esetében a tényleges különböző gyökerek Jordan blokk nézne ki:
Tegyük fel, hogy többek között a valós sajátértékei van többszörösei. Jordan cella lesz az alábbiak szerint:
Például, ha a multiplicitása k = 2, a Jordan blokk mátrixot felírható a következőképpen:
Ha a sok k = 3, a Jordán blokk mátrixot felírható a következőképpen:
Ha a három sajátértékek
a gyökerek a multiplicitás 2, a Jordán formája a következő:
Ha a két sajátértékei A komplex konjugált, rögzítése Jordan blokk nézne ki:
- a képzetes része a sajátérték
.
Megtalálható egy általános megoldása az inhomogén rendszer a következő képlet segítségével: