Párhuzamosítását több bites ábrázolása a számok a moduláris adatstruktúrák -

Párhuzamosítás REPRESENTATIONS több számjegyű számokkal a moduláris felépítés DATA

1. Orvosi Egyetem „Szurgut State University”

A dokumentum ismerteti a párhuzamosítását reprezentációi szuper-nagy több-bites számok segítségével a maradék osztályok rendszer (CRS), a kínai maradéktétel (CTO) és kis Fermat-tétel. Egy ilyen több bites számok ábrázolása ad előnyt adott időben a számítási műveletek jóval nagyobb adatmennyiség feldolgozását, mivel minden információ feldolgozása zajlik párhuzamosan, egymástól függetlenül. Párhuzamos nézet lehetővé kijelző egy millió, vagy több jegyű számok és széles körben lehet használni a kódolás az információ ultragyors számítási algoritmusok és tesztelési szuperszámítógépek. Annak ellenére, hogy néhány hiányosságot, ami lehet legyőzni, moduláris rendszer, vagy a rendszer maradék osztályok egy egyedülálló matematikai környezet párhuzamos számítástechnika. Ezért ez a rendszer figyelembe kell venni a tervezés során nagy teljesítményű rendszereket alapul programozható logikai integrált áramkörök (FPGA) és a többmagos processzorokat.

Kínai maradéktétel

Kis Fermat-tétel

maradék osztályok rendszer

1. Amerbaev VM Elméleti alapjait számítógépes aritmetika. - Alma-Ata, Nauka, 1976. - 320 p.

2. Buchstab AA Számelmélet. - M. Science 1975.

3. Vaszilenko ON Modern módszerek Prímtesztelés // Cybernetic gyűjtemény. Új sorozat. - 1988. - Vol. 25. - P. 162-187.

A mai algoritmikus elmélet a nagy és nagyon nagy számban fontos szerepet játszanak a kriptográfia építésére ciphers különböző összetettségű és teljesítményének vizsgálatára szuperszámítógépek [4, 8]. Vizsgálata extra nagy számok [5] azt mutatta, hogy azok értéke, amelyeket nehéz vagy szinte lehetetlen elképzelni, hogy a apránként a szokásos helyzeti számrendszert.

Ha a szám A = 22147483647 emelte a megadott teljesítmény, akkor több mint egymillió bit. Ezért ezt a számot nem megfelelő általánosítható Helyiérték valós kezdeti állapotban.

Ábrázoljuk a rendkívül nagy több-bites számok hagyományos pozícionális számrendszer, formájában az információs rendszer reakcióvázlaton szemléltetett kiszámításakor ultralarge számok (ábra. 1), és elemzik azokat.

A diagram azt mutatja, hogy a bemeneti a számítási algoritmus ultralarge számok (bal nyíl) jönnek a rendkívül nagy több-bites számok, nyilak „felülről lefelé” kifejezések pozicionális számrendszer és aritmetikai műveletek. A kimenet az algoritmus-szám ultralarge eredményt. Azonban, ha a találatok számát megjeleníteni a normál helyzeti rendszer, vannak problémák:

1. A szám nem fér bele egy normál számítógép a [0. 231].
2. Az eltöltött idő számok ábrázolása generalizált helyzeti rendszerben.
3. A terhelés a RAM, ha a szám alkotja kapcsolt listák.

Az A reakcióvázlat leszakító igen nagyszámú több bites (ábra. 2) szerezhetők be a kimenet a száma szuper-nagy, ami nem fér be egy tipikus számítógép tartományban. Vizuálisan végez semmilyen műveletet ezzel a számmal nem lehetséges, mivel úgy száz oldalnyi fájlok bármilyen típusú a Windows operációs rendszer.

Ezzel kapcsolatban extra nagy multi-bites számok A = 22147483648 hatékonyan jelen nonpositional radix - maradék osztályok rendszer, ahol nincs carry alacsonyabb értékű bit a magasabb.

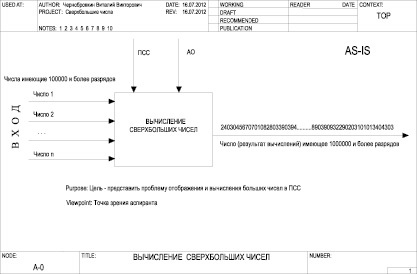
Ábra. 1. A rendszer számok kiszámítására Superlarge

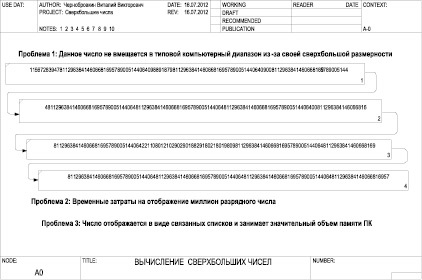
Ábra. 2. sematikus ábrázolása a nagy absztrakt jegyű szám formájában kapcsolt listák

Van egy probléma, ami a következő: ha a szuper-nagy jegyű számot képviseli maradék osztályok rendszer [5, 7], a maradékok száma, valamint a kiválasztott rendszer bázis nagy lesz, ami viszont hatással van a számítási folyamatokat.

Bemutatjuk számtartományként bináris helyzeti rendszer [265537. 22147483648].

Elfogadása 1 A = száma 22147483648, amelynek szám bitek a tartományban [265.537. 22147483648] vagy több, lehet nevezni extra nagy jegyű szám.

Száma, amelyek egy millió, vagy több bit nevezhetjük extra nagy multi-bit, mivel ez egy nagy számérték valós teljesítményt.

Elfogadása 2 Superlarge több-bites számok képviselik a maradék osztályok rendszer súlyától függ a pozicionális rang | Z | P [1], és így állhat egy nagy több kiválasztott modulok és maradékok, ill. Súly helyzeti rang | Z | P tartalmától függ számának prímszám. Kiszámításakor az extra nagy számban maradék osztályok rendszer figyelembe kell venni a következő egyenletet:

ahol A - számos számítási eredményre; - az alapja a moduláris rendszer viszonylag fix.

Elfogadása 3 ultralarge száma leírható a maradék osztályú rendszer formájában maradékainak maradékot [3, 5, 6, 7]

egy ≡ b (mod p). (2)

Az a lehetőség, egy ilyen ábrázolása a szám határozza meg a következő tételek.

1. Tétel (Kínai maradéktétel) [2, 3, 5, 6, 7].

Bármilyen pozitív egész szám a maradék osztályok rendszer képviseli, mint egy sor maradékok (maradék) számát elosztjuk a választott bázis (modulok) rendszert.

Bizonyítás: Legyen A = szám 22147483648 jelennek meg a rendszerben, mint a maradék osztályok

ahol A1, A2, ..., egy - legkisebb nem-negatív maradékok (maradékok) által alkotott egész körzet egy a választott bázis

ahol pi - viszonylag elsődleges.

Ha a képviselet a szám (3) csak akkor biztosított

Ezután a szám egy a következő:

Egy ≡ a1 (mod p1);

Egy ≡ a2 (mod p2); (7)

A ≡ egy (mod pn).

Tétel 2 Ha több pi = p1, p2. pn viszonylag fix, akkor bármilyen maradék a1, a2. egy, oly módon, hogy 0 ≤ egy ≤ pn, minden i = 1, 2 n létezik egy számot A, amely, ha osztva pi hozamok maradékot ai minden i = 1, 2 n

Bizonyítás: Teljes indukciót alkalmazunk tovább. Az n = 1 az állítás nyilvánvaló. Tegyük fel, hogy a tétel érvényes n = k - 1, azaz, létezik egy számot M, így ri fennmaradó amikor osztva nA pi i ∈. jelent

d = a1, a2. ak-1. (8)

Tekintsük a számok M, M + d, M + 2d. M (ak - 1) d. Megmutatjuk, hogy legalább az egyik ezek a számok a maradékot adja, ha elosztjuk rk ak. Tegyük fel, hogy nem ez a helyzet. Mivel a mennyiség a számok egyenlő AK, és az esetleges maradék nem lehet több, mint ak elosztjuk be ezeket a számokat AK - 1 (mivel sem a számok nem ad maradékot rk), akkor két szám, amely azonos maradékok közöttük. Legyen ez a szám

M + M + TDM SDI 0 ≤ s ≤ AK

és 0 ≤ t ≤ ak és s ≠ t. (9)

különbségük

(M + sd) - (M + td) = (s - t) d

Meg van osztva ak, ami lehetetlen, hiszen 0 <s – t 

Mivel mi beszélünk millió számjegyű szám, akkor írja le az igazi problémát a megépítésük maradék osztályú rendszer:

• Kiválasztása bázisok száma
• Bit kiválasztott bázisok
• több bites maradékok

Ez azt jelenti, hogy ha építünk rendkívül nagy számú, hogy van egy millió vagy több számjegy, a bázisok száma függ majd a kis mélységben ezeket a számokat. Például, ha a szó mindegyikének hossza a kiválasztott kis bázis, illetve a bázis mennyisége növelni kell. Ezzel szemben, ha a kiválasztott bit nagy ok, akkor csökkenteni kell a kívánt számot. Beszélünk a tágulás vagy összehúzódás a bázisok a rendszer maradék osztályok [7]. A másik probléma az, hogy amikor megjeleníti a nagyszámú A = 22147483648 reziduális osztályozási rendszer maradék is lehet multi-bit.

Általánosságban, a fenti problémák megoldhatók segítségével kis Fermat-tétel, amelynek bizonyítéka van megadva [2, 6] és a kínai maradéktétel [2, 3, 5, 6, 7].

Az alapvető jelentése kis Fermat-tétel, hogy ha p - pozitív prímszám, a - egész, akkor

ap-1 ≡ 1 (mod p), ha p - prímszám (10)

Ez azt jelenti, ak ≡ ar (mod p), és nem elegendő számítási csak az exponenciális, amelynek mértéke kisebb, mint p - 1.

A kínai maradéktétel egyszerűbbé tesszük a kijelző extra nagy számban. Megmutatják nekik, mint a hatalom maradék modulo n, ha ismerjük a prímfaktorizáció. Tegyük fel, hogy minden elsődleges tényező ebben a kiegészítőben jön sokaságának 1, mert ebben az esetben az eljárás a leghatékonyabb.

Tegyük fel, hogy a bővítés formában van

ahol 0

Mert egész számokat és m először megtalálni AM levonás minden modulhoz pi. Ha az elsődleges tényezők nem túl nagy, akkor a számítás nagyon gyors lesz még a nagy m, és, mert segít nekünk, hogy Kis Fermat-tétel (10. o.).

Feltételezve, hogy a számítások tenni, és

am ≡ r1 (mod p1) és 0 ≤ r1 ≤ p1;

am ≡ r2 (mod p2) és 0 ≤ r2 ≤ p2; (12)

am ≡ rk (mod pk), és 0 ≤ rk ≤ pk.

Ezért, hogy meghatározza a levonás am modulo n kell megoldani a rendszer összehasonlítás:

Emlékezzünk vissza, hogy a modulok a rendszer - különböző páros relatív prím számokat. Ennélfogva, a kínai maradéktétel, a rendszer mindig egy oldat, például R, 0 ≤ ri ≤ pi - 1. Továbbá, bármely két ilyen oldatok egybevágó modulo p1. pk = n .... Mivel am is egy megoldás a rendszer, hogy van am ≡ r (mod n). Következésképpen, R - ampo maradékot modulo n.

Példa. Surjectively számának megjelenítéséhez 22147483648 A = A kiválasztott maradék bázisok p1 = 11, p2 = 13, p3 = 17, p4 = 19. változó mértékét az említett egységek száma 2147483648-1 = 2147483647 Kis Fermat-tétel alkalmazható, amelyhez talál maradékok modulo fokú 2147483647 (a p1) az egyes kiválasztott bázis p1, p2, p3, p4. majd

pi-1 = 11 - 1 = 10; pi-2 = 13 - 1 = 12;

pi-3 = 17 - 1 = 16; pi-4 = 19 - 1 = 18; (14)

a'1 = 2147483647 = 10 mod 7;

a'2 = 2147483647 = 12 mod 7; (15)

a'3 = 2147483647 mod 16 = 15;

a'4 = 2147483647 MOD 18 = 1.

22147483647 ≡ a1 = 27 (mod 11);

a2 = 22147483647 ≡ 27 (mod 13); (16)

a3 = 22147483647 ≡ 215 (mod 17);

≡ 22147483647 a4 = 21 (mod 19).

Végül a száma A = 22147483647 fog kinézni:

27 ≡ 7 (mod 11);

27 ≡ 11 (mod 13); (17)

215 ≡ 9 (mod 17);

2 ≡ 2 (mod 19).

1. párhuzamosítás reprezentációk ultralarge több bites számok segítségével a maradék osztályok a rendszernek az az előnye, hogy idő számítások nagy mennyiségű adatot kell feldolgozni, mint az összes adatfeldolgozás történik párhuzamosan és egymástól függetlenül.

2. Minden jegyű szám is képviselteti formájában maradékainak teljesítmény maradványok.

3. Fent a számok képviselik párhuzamos módon lehet elvégezni gyorsított párhuzamos számítástechnika.

4. Ha a formáció ai maradékok előállított egymástól függetlenül, minden számítás akkor is bekövetkezik, egymástól függetlenül.

Inyutin SA dts Professzor „Design számítógépes rendszerek” VPO „Orosz Állami Műszaki Egyetem. KE Ciolkovszkij (MATI)”, Moszkva;

Baharev MS dts Professzor "Oil and Gas Business" VPO "Szurgut Oil and Gas Intézet, Tyumen State Oil and Gas University ág" Szurgut;

Krishtop VV Prof. egyetemi tanár, "fizika", Far Eastern State University szállítás, Habarovszk, a professzor a University Kwangwoon University, Korea.

Mi hozza meg a folyóirat által közzétett Publishing House "The Academy of Natural Sciences"

(High impakt faktor RISC, folyóiratok téma, amely minden tudományos területen)

Tudományos folyóirat | ISSN 1812-7339 | PI №77-63397

Műszaki információs - [email protected]

Ügyvezető titkára a folyóirat Bizenkova MN - [email protected]

Magazin tartalom elérhető a Creative Commons «Nevezd» engedély ( „Nevezd”) 4,0 világ.

Kapcsolódó cikkek

• Összehasonlítása több számjegyű számokkal