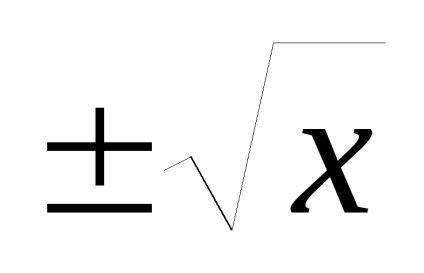Oenie menetrendek páros és páratlan függvények

Mint már említettük, egy még funkciója y = f (x) a teljes körű variációs argumentuma a kapcsolatban f (x) = f (- x). Következésképpen a funkciója ennek a fajta veszi az azonos érték értékekből az az érv, egyenlő nagyságú, de ellentétes előjelű lesz. Szánjon legalább egy páros függvény szimmetrikus az ordináta.

Felrajzolásához egy még függvény y = f (x) kell építeni egy ága a grafikon ezt a funkciót csak a régióban pozitív x értékei

. A grafikon y = f (x) a negatív tartományban a érvelés szimmetrikus ágaznak épített ordináta és a gondolkodás kapunk képest erre a tengelyre.

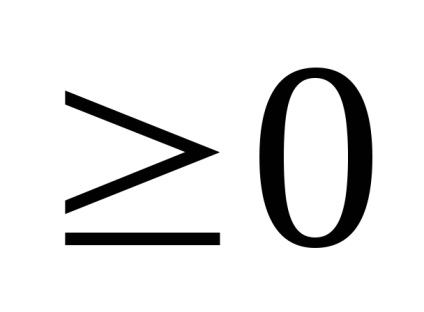
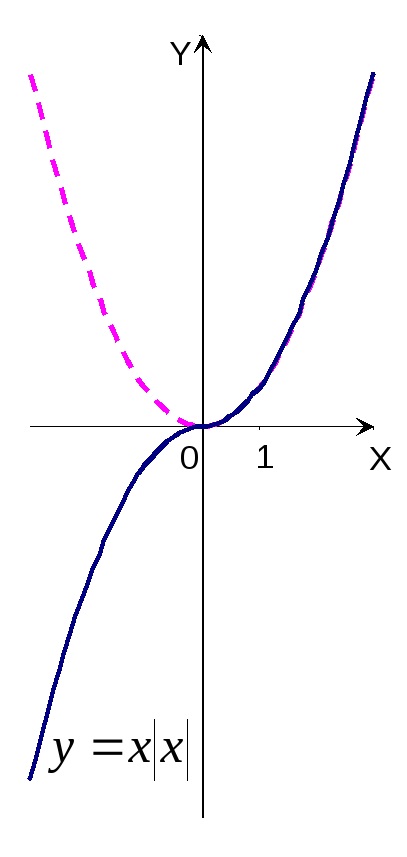
8. példa Plot a függvény az y =

.

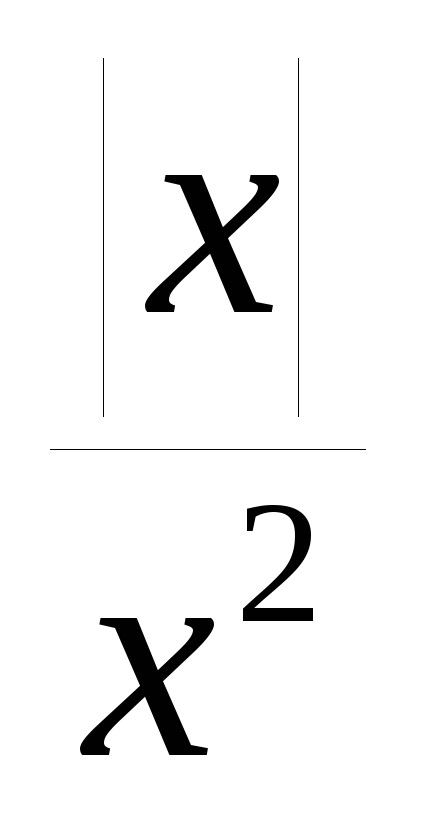
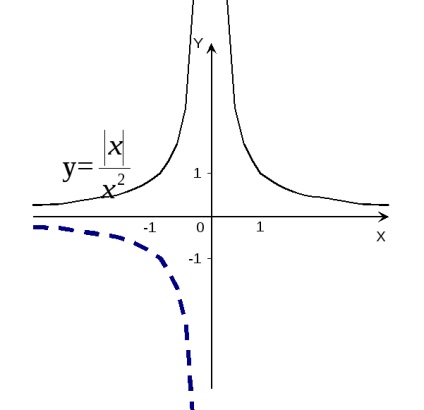
R e w n e: Ez a funkció - még, ezért elegendő össze egy ütemtervet a régióban a pozitív értékek x (x = 0 pont nem szerepel a funkció tartomány). Amikor x> 0 az eredeti függvény a y =

. Graph funktsiiy =a negatív znacheniyx szerezni reflexió az Y-tengely (11. ábra).

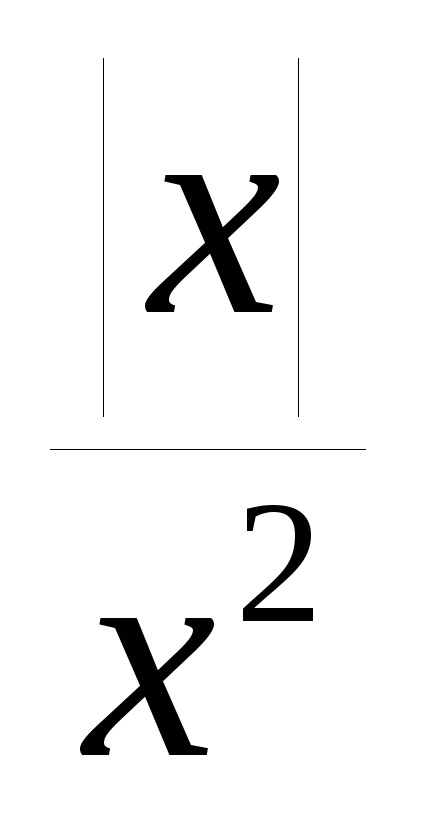
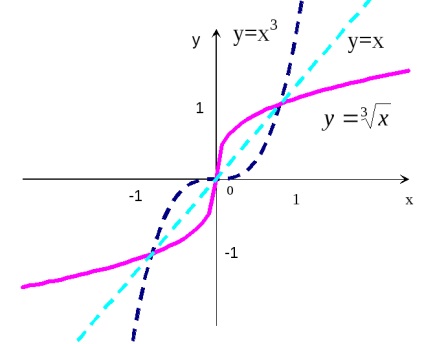
A páratlan függvény az y = f (x) a régió valamennyi értékének érv egyenlőséget f (-x) = -f (x). Így a régióban a negatív értékek az érvelés ordináta grafikon páratlan funkciók azonos nagyságrendű, de ellenkező előjellel az ordinátán a grafikon ugyanazt a funkciót, mint a megfelelő pozitív értékeit x. Graph páratlan függvény szimmetrikus az eredetét.

Felrajzolásához páratlan függvény az y = f (x) kell kialakítani ága a grafikon ezt a funkciót csak a régióban a pozitív értékek az érvelés (X

).

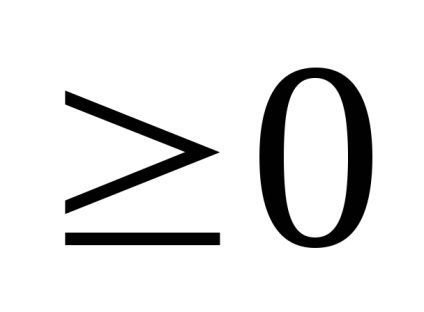
A grafikon y = f (x) a régióban a negatív értékek az érvelés szimmetrikus kialakítva ága képest a származási és előállíthatók a reflexió az ágak tekintetében az ordináta tengelyen, majd egy reflexió a régióban a negatív értékek az x tekintetében az abszcissza.

9. példa Plot függvény az y = x

.

P e w n e: a kezdeti funkció páratlan, tehát, hogy építeni a pozitív argumentum egy (X

), Ahol azt a y = x 2 A grafikon y = x a régióban a negatív értékek az érvelés tükröződik kialakítva ága képest eredetű (12. ábra).

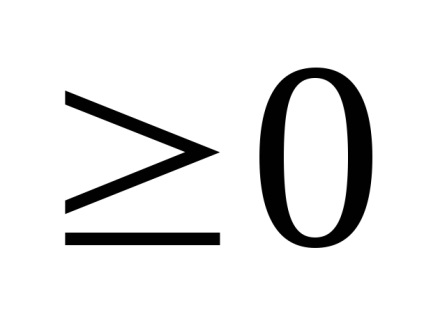
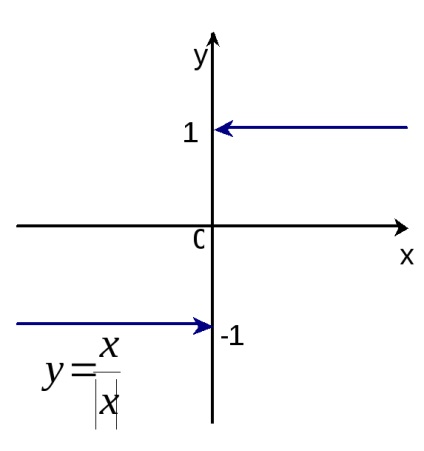
10. példa Plot a függvény az y =

.

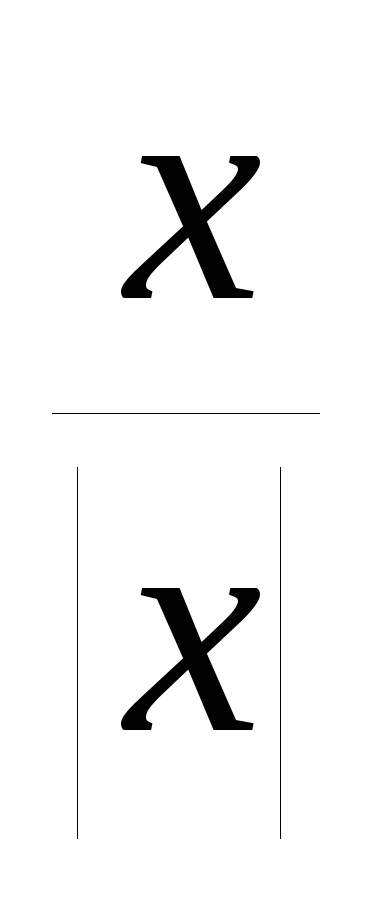
R e w n e: Ez a funkció páratlan, ezért épület ütemezése csak a régióban x> 0 (az a pont x = 0 nem szerepel a függvény tartomány), ahol azt a y = 1. Branch a függvény grafikonját az x<0 получаем отражением относительно начала координат построенной ветви кривой (рис.13). Стрелки означают, что точки (0,1) и (0,-1) не принадлежат графику.

2.4. Építése inverz függvény grafikonján

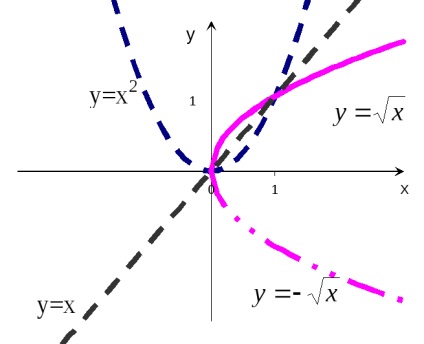
A direkt és inverz függvények kifejezni ugyanazt kapcsolat a változók között az x és y, azzal az egyetlen különbséggel, hogy a fordított függvényében ezeket a változókat változott, amely egyenértékű a változó a koordinátatengelyek megnevezések. Ezért az inverz függvény grafikon szimmetrikus közvetlen grafikus funkciókat relatív felezővonal

I. és III kvadránsban, azaz tekintetében a y = x. Így megkapjuk a következő szabályt.

A konstrukció a grafikont a funkció y =

, inverz hogy funktsiiy = f (x), meg kell építeni a grafikon y = f (x) és hogy az tükrözze a viszonylag egyenes y = x.

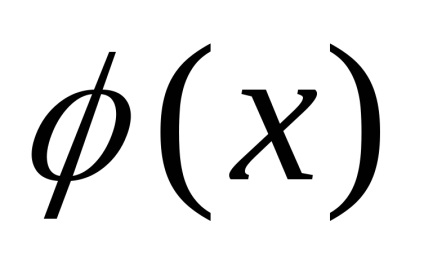
11. példa Plot a függvény az y =

.

R e w n e: CH

A konstrukció a grafikon ennek a funkciónak, úgy a grafikon parabolyy = x 2 (14. ábra - szaggatott görbe) és a menetrend annak inverz függvény az y =, kapott viszonylag egyenes reflexió parabola y = x. Az inverz függvény két értékű. Tekintettel arra, hogy az eredeti funkció y =egyértelmű és hatókörét változás intervallum 0y<, ütemezés funktsiiy =A felső ág tükröződik parabola (folyamatos vonal). Az alsó ága (két-pontozott vonal) egy grafikon funktsiiy = -.