Fresnel diffrakció egyszerű akadályok
Diffrakciós egy kör alakú nyílás. Tekintsük diffrakciós konvergáló sugarak, vagy Fresnel diffrakció végzett abban az esetben, ha a diffrakciós mintázat figyelhető meg véges távolság az akadályok okozta diffrakciós.
Pose az útját a gömb alakú hullám fény átlátszatlan képernyőt egy kerek lyuk sugara. A képernyő van elhelyezve, hogy a merőleges S egy átlátszatlan képernyőn, esik pontosan a közepén a lyuk (ábra. 17.13).
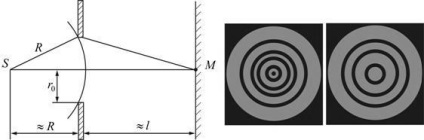
A folytatása ennek merőleges hogy egy M pont, és átgondolni, hogy mi fogjuk látni a képernyőn.
Osztjuk a nyitott része a hullám Fresnel zóna a felületen. Részletek a diffrakciós minta számától függ Fresnel zóna nyit a nyílást. A amplitúdója a kapott oszcilláció izgatott minden zónában az M
Így, amikor a furat kinyílik páratlan számú Fresnel zónák, az amplitúdó (intenzitás) át az M pont nagyobb lesz, mint a szabad terjedési hullám; Ha még. az amplitúdó (intenzitás) egyenlő nullával, ábrán látható. 17.13.
Természetesen, ha. akkor nem diffrakciós minta nem.
A diffrakciós a lemezen. Gömb alakú hullám szaporító egy pontban találkozik S. útban meghajtó (ábra. 17,14).
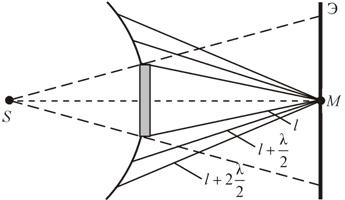

M fekszik a merőleges a lemez középpontja. Az első Fresnel zónában alapul a tárcsa pereme, és így tovább. D.
A rezgés amplitúdója fény az M pont felével egyenlő az amplitúdó miatt az első nyílt területen. Ha a lemez mérete kicsi (borító kis számú zóna), az intézkedés az első zóna kissé eltér a központi terület a hullámfront. Így a megvilágítás a ponton M azonos mivel annak hiányában a képernyő. Mivel a szimmetria a központi fénypont lesz gyűrűjében a fény és az árnyék (határain kívül a geometriai árnyék).
Paradox első pillantásra, azt a következtetést, amelynek értelmében a közepén a geometriai árnyék lehet egy fényes pontot hozta Poisson 1818-ban és később róla nevezték el. „Arago spot” megerősíti a helyességét Fresnel elmélete.
17.7. Diffraction párhuzamos sugarak (Fraunhofer diffrakciós)
diffrakciós típusú, amelyben a diffrakciós mintázat van kialakítva párhuzamos sugarak. Ez az úgynevezett Fraunhofer diffrakciós. Párhuzamos sugarak lesz látható, ha a forrás és a képernyő a végtelenben. Majdnem két használt lencsék: középpontban egy - egy fényforrást, és a hangsúly az egyéb - a képernyőn.
Bár elvileg Fraunhofer diffrakciós nem különbözik a Fresnel diffrakció, de a gyakorlatban ez az eset azért fontos, mert ez a fajta diffrakciós használják sok eszköz diffrakciós (diffrakciós rács, például). Ezen kívül van egy matematikai számítás könnyebb, és lehetővé teszi számunkra, hogy megoldja a problémát, mielőtt a végén a mennyiségi (Fresnel diffrakció vettük minőségileg).
Diffrakciós fényében egyetlen rés. Hagyja folyamatos képernyő van egy rés: a rés szélessége. rés hossza (merőleges a lemez síkjára) (ábra. 17.15). A rés-beeső párhuzamos fénysugarak segítségével. Az egyszerűbb számítás azt feltételezzük, hogy a rés a síkban AB az amplitúdó és fázis az esemény hullámok azonosak. Osztjuk a nyílásba a Fresnel zónában úgy, hogy az optikai útvonal közötti különbség jövő fénysugarakat a szomszédos zónák, egyenlő volt.
Ha a rés szélessége határozza páros számú zónák, akkor a pont (fókusz oldalon) lesz egy minimális intenzitású, és ha páratlan számú zónák, a maximális intenzitás:
- feltétele a minimális intenzitás;