taxi geometria
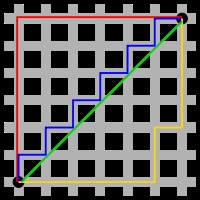
A városi területeken a metrikus hossza a piros, sárga és kék vonalak egyenlő (12). A euklideszi geometria zöld vonal hossza 6√2 ≈ 8,49, és egyetlen legrövidebb út.
Taxi geometria - mutatót. Hermann Minkowski fent megadott. Szerint ez a mutató, a két pont közötti távolság összege abszolút különbségek azok koordinátáit.
Ebben a mutatóban sok nevet. Taxiautók geometria is ismert, mint a Manhattan távolságot. metrikus tér a város. L1 norma vagy metrikus ℓ 1> (lásd. Lp tér) metrikus városrésztől. metrikus taxi. Manhattan mutatót. téglalap metrikus. metrikus derékszög; Z 2> ez az úgynevezett rácsok metrikus és metrikus-4 [1] [2] [3].
Körök a diszkrét és folytonos geometria háztömbök
Város blokkok d távolság 1> két vektor p. q, \ mathbf> n dimenziós valós vektorteret egy előre meghatározott koordináta-rendszerben - a hosszúságok összegét kiugrások közötti szegmenst a pontokat a koordinátatengely. FormálisabbanManhattan távolság függ a forgási koordináta-rendszert, de nem függ a tükörképét a koordináta tengelyen vagy a közlekedés. A geometriában alapján Manhattan távolság, megfelel minden Hilbert axiómák. kivéve az axióma egybevágó háromszögek.
A labda ez a mutató alakja van egy oktaéder. akinek csúcsai koordinátatengelyeken.
Manhattan távolság két mező között a sakktábla a minimális számú mozog, ami kell vezír. mozgatni az egyik mezőről a másikra.
Távolságokat sakk
A távolság a sakktábla mezők Vizier (vagy Rook, ha a távolság száma sejtekben.) Megegyezik a Manhattan távolságot; Király és királyné Chebyshev távolságot. és elefánt - Manhattan távolság a táblán, 45 ° -ban elfordítható.
Összeg Manhattan közötti távolságok a csuklót és a helyzetben, amelyben megoldani puzzle „Tizenöt” használják, mint a heurisztikus függvény megtalálni az optimális megoldást. [5]
sejtautomaták
A cellák sokaságát egy kétdimenziós négyzet padlóra. Manhattan távolság kisebb, mint az r a sejtből. nazvaetsja Neumann szomszédságában tartományban (sugár) R [6].