Módszerek megoldására differenciálegyenletek
Megoldásában tudományos és műszaki problémák gyakran van szükség, hogy matematikailag leírni a dinamikus rendszer. Ezt a legegyszerűbben formájában differenciálegyenletek (DE), vagy a rendszer differenciálegyenletek. Leggyakrabban ezek olyan probléma merül fel problémák megoldásában kapcsolatos modellezése a kinetikája kémiai reakciók és a különböző közlekedési jelenségek (hő, tömeg, lendület) - hőátadás, keverés, szárítás, adszorpció, a mozgását leíró makro- és mikro-részecskék.
Egyes esetekben, a differenciálegyenlet átalakítható a formában, amelyben a vezető származék kifejezését. Ezzel a jelöléssel nevezzük az egyenlet megoldható a legmagasabb származékot (így vezető származék hiányzik a jobb oldalon az egyenlet):
Megoldása közönséges differenciálegyenletek függvénye y (x), amely minden x kielégíti ezt a függvényt egy bizonyos véges vagy végtelen intervallumban. A folyamat megoldása differenciálegyenlet nevezzük integráció differenciálegyenletek.
Történetileg az első és legegyszerűbb módja a numerikus megoldása a Cauchy probléma dlyaODU elsőrendű Euler módszer. Ez alapján a közelítés a származékos véges lépésekben eltartott arány (y) és a független (x) változó közötti egyenletes rács csomópontok:
ahol yi + 1 a kívánt érték a függvény a ponton xi + 1.
Euler módszer pontossága javítható használatát a beépített közelítés pontosabb képlet integrációs -formula trapéz.
Ez a képlet vélelmezett képest yi + 1 (az érték a bal és a jobb kifejezés), hogy egy olyan egyenletet képest yi + 1. eldönteni, hogy melyik lehet, például, számszerűleg bármilyen iteratív módszer (ebben a formában lehet tekinteni, mint egy olyan iteratív képletű egyszerű iterációs módszer).
Összetétel tanfolyam: A tanfolyam három részből áll. Az első részben egy rövid leírást a módszereket. A második részben a készítmény, és a probléma megoldására. A harmadik rész - a szoftveres megvalósítása a számítógépes nyelv
A cél természetesen a munka: a tanulmány két megoldási módjait, differenciálegyenletek módszer Euler-Cauchy és jobb metodEylera.
1. Az elméleti rész
A közönséges differenciálegyenletek (ODES)
Differenciál egyenletek parciális származékok.
Közönséges differenciálegyenletek az egyenlet azok, amelyek tartalmaznak egy vagy több származékát a funkciója ismeretlen. Ezek felírható
A legmagasabb rendű tartozik a (1) egyenlet az úgynevezett a sorrendben a differenciálegyenletek.
A legegyszerűbb (lineáris) egyenlet TAC (1) a sorrendben a származékos permited
Megoldás A differenciálegyenlet (1) bármely olyan függvény, amely után szubsztitúció az egyenlet kiderül, hogy a személyazonosság.
A fő probléma a lineáris probléma az úgynevezett TAC Kashi
Megoldást találni a (2) egyenlet függvényében a kezdeti feltételeket (3)
Geometriailag, ez azt jelenti, hogy meg akarja találni az integrál görbét ponton halad át) teljesítéséhez (2) egyenlet.
Numerikus a célkitűzések Kashi szükséges eszközökkel össze egy táblázatot az értékek az kielégíti a következő egyenletet (2), és a kezdeti feltétel (3) az intervallum egy bizonyos lépés. Ez általában feltételezzük, hogy ez a kezdeti feltétel van beállítva a bal végén a szegmens.
A legegyszerűbb numerikus módszerek megoldani egy differenciálegyenlet az Euler módszer. Ez alapján az elképzelést, létrehozunk egy grafikai megoldások differenciálegyenletek, azonban ez a módszer, amely mind egy módja a megállapítás a kívánt funkciót a számszerű formában vagy asztalra.
Tekintsük a (2) egyenlet az eredeti állapot, azaz feladata Kashi. Nézzük megoldani a következő problémát az elején. Megtalálni a legegyszerűbb módja, hogy a közelítő értéke az oldat egy olyan ponton, ahol egy kellően kis lépés. (2) egyenlet együtt a kezdeti feltétel (3) által meghatározott érintő iránya a kívánt szerves görbe koordinátái
tangens egyenlet
Mozgó mentén az érintő, akkor kap egy hozzávetőleges értéke a megoldás azon a ponton:
Egy közelítő megoldást a ponton akkor ismételje meg az eljárást a korábban leírt: építeni egy átmenő ezen a ponton egy lejtőn, és rajta találni egy közelítő értéket a megoldás azon a ponton,
. Megjegyzendő, hogy ez a vonal nem érinti a valódi integrált görbe a ponton nem állnak rendelkezésre, azonban, ha elég kicsi ahhoz, hogy megkapta a közeli a pontos értékeket a megoldás.
Követve ezt az ötletet, építeni egy rendszert egyenlő távolságban lévő pont
Előállítása értéke táblázata a kívánt funkció
Euler módszer abban áll, a ciklikus képlet alkalmazását
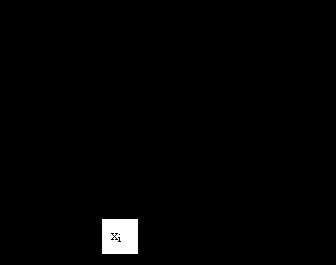
1. ábra grafikus értelmezése Euler módszer
Módszerei Numerikus integráció differenciálegyenletek, amelyben a döntéseket nyert egyik csomóponttól a másikig az úgynevezett lépésről lépésre. Euler módszer a legegyszerűbb képviselője körökre módszerekkel. A jellemzője bármely lépésében a módszer lényege, hogy mivel a második lépésben, a kezdeti értéket a (5) képletű maga közelítő, vagyis hiba minden lépésben növekszik szisztematikusan. A leggyakrabban használt módszer, hogy értékelje a pontossága a módszerek közelítő inkrementális numerikus megoldása módszer ODE dupla áthaladás egy előre meghatározott hosszúságú hangmagasság és a hangmagasság
1.1 javított Euler módszer
Az alapötlet ennek a módszernek: számítják képletű (5), a következő érték pontosabbak lesznek, ha a származék értéke, vagyis a meredeksége egyenes szubsztitúciós integrál görbéből a szegmens nem kell számítani a bal szélén (azaz, pont), és a középső szegmens. De ahogy az érték a származékos pontok közötti nem számítjuk, akkor lépni a különálló területeken a központ, amely az a pont, az egyenes egyenlete lesz a következő formában:
Egy általános képletű (5) a forma
A (7) bekezdése csak azokra következésképpen megkapja az értékét lehetetlen azonban találni Euler, így kapunk pontosabb eredményt kaptak az alábbiak szerint: kezdve az (5) értéke
Pontjában, majd a következő képlettel (7) lépésekben
Miután további számítási eredményeket, amikor végre az alábbi képlet szerint (7)
1.2 Euler-Cauchy módszerrel
Geometriailag ez azt jelenti, hogy az elejétől határozza meg az irányt a integrál görbéből a vonatkozási pont, és egy kisegítő pont, és a végső átlagos értéket veszi irányok ilyen irányban.
2. készítmény és a probléma megoldása
Hogy oldja meg a differenciálegyenlet javult Euler módszer és az Euler-Cauchy módszerrel példában STP egyenletben
2.1 Megoldás A javított Euler módszerrel
Hogy oldja meg a differenciálegyenlet Euler javított eljárás az egyenlet belül STP
egy lépést. találunk:
Vegyük például az egyenlet STP pontossággal.
Az eredmény a program a 2. ábrán látható az a) és b):
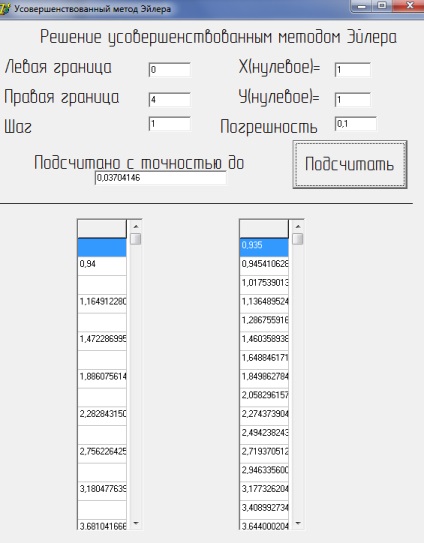
2. ábra a) Értékesítési számítógépes teszt továbbfejlesztett
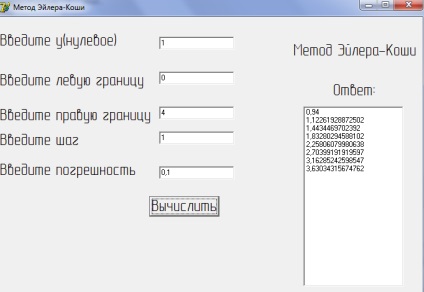
2. ábra b) végrehajtása a számítógép teszt esetében az Euler-Cauchy módszerrel
Mint ismeretes előre, a megoldás, és ez egybeesik a kapott eredmény a programban, arra lehet következtetni, hogy a program megfelelően működik.
Ha meg a> b, akkor a program megy a következő:
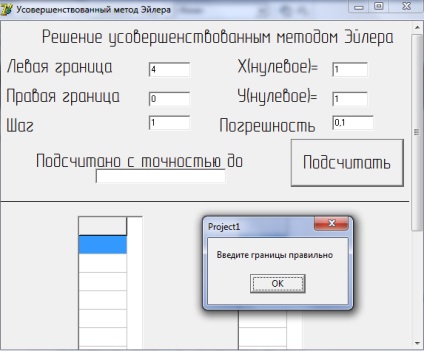
3. ábra - Eredmények megoldások egyenlet javult Euler módszer bevezetésével a> b
4. ábra - eredménye egyenlet megoldásai az Euler-Cauchy módszerrel beadva> b
Ha a hiba nem helyes, a program következőképpen kell eljárni:
5. ábra - Az eredmény az egyenlet megoldása javult Euler módszert, ha nem megfelelően adagolt hibát
6. ábra - Az eredmény a döntés Euler-Cauchy módszer, ha nem megfelelően vezetett hibák
3.4. A döntés szerint a számítógép probléma
Vegyük például az egyenlet STP pontossággal.
Amikor megoldása egy adott egyenlet nyelvén Borland Delphi programozás, megkapjuk a következő eredményeket (3. ábra):
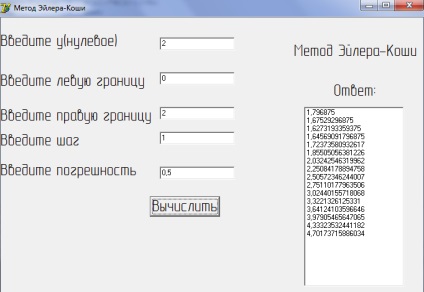
Ábra 7Realizatsiya on EVMmetoda Euler-Cauchy
Vegyük például az egyenlet STP pontossággal.
Amikor megoldása egy adott egyenlet nyelvén Borland Delphi programozás, megkapjuk a következő eredmények (4. ábra):
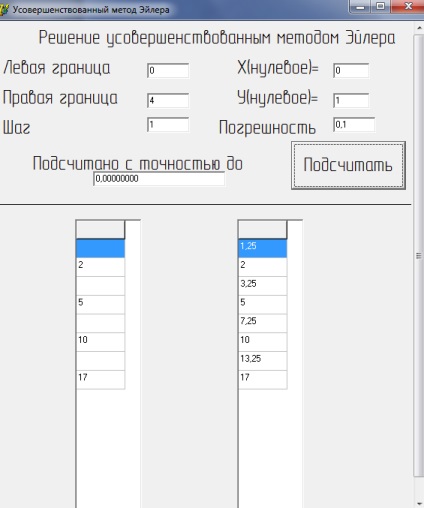
Ábra 8Realizatsiya számítógépen Euler usovershenstvovannogometoda
1. és 2. táblázat a kiadási programok beállításával különböző kiindulási adatokat.
1. táblázat - munka eredményei program javított Euler módszer
következtetés
Így világos, hogy a számítás a differenciálegyenlet módszerrel Euler-Cauchy és javított Euler módszer megoldás nem adja meg a pontos értéket, de csak közelíteni.
Minél kisebb az intervallum beállítása lépést és számítási műveleteket, annál pontosabb a kapott eredmény gép. A nagyobb pontosság érdekében szükséges egy nagyobb számú iteráció, ami a költségek emelkedése az integrálási idő számításánál a számítógép fordítottan arányos számítás pontosságát.
Felhasználási egyszerre kiszámításához két lehetséges módszer, hogy vizsgálja meg a függőség a pontosabb számításokat, ha mindkét módszer. Mit tehet egy határozott következtetést, hogy a javított Euler módszer könnyebb a gép, és az eredmény (ami nagyon közel van a pontos), hogy gyorsabb módszer Euler-Cauchy. De Euler-Cauchy módszer pontosabb.
Írt programok Borland Delphi megoldására differenciálegyenletek. A kapott oldatot működik programok egybeesik a választ a példa
Listája használt irodalom
Samara AA Gulin AV Numerikus módszerek: Tanulmányok. utasítás az iskolák számára. - M. Science. Ch. Ed. Fizika és matematika. Irodalom. 1989 - 432 p.
Kapcsolódó művek:
Iteratsionalnye metodyresheniya nemlineáris egyenletek
). Besorolás metodovresheniya differentsialnyhuravneny és numerikus módszerek az integráció. A koncepció a Cauchy probléma, és az integráció lépést. A módszer az egymást követő közelítések (Piccard módszer). MetodEylera.
Euler. Euler fejlesztette tovább differentsialnyhuravneny elmélet. megkezdődött a munka a Leibniz és Bernoulli. Elmélet differentsialnyhuravneny. Cauchy létre. Morse távíró létrehozott egy korszerű, c. A módszer a „próba és tévedés” a döntés eszköz.
Módszerek a számítástechnika és azok alkalmazása a fizikai problémák
Példa - differentsialnoeuravnenie a kiindulási körülményekhez. Összesen resheniedifferentsialnogouravneniya ott. 1 ... m - száma egyenletek. k - számos korábbi számítás pontot. UsovershenstvovannyymetodEylera -Koshi specifikáció. Ez a módszer azon alapul.
Cheat Sheet >> Számítástechnika, programozás
megbízhatóságának javítása a végrehajtás iránti kérelmek, amely korszerű, 32 bites komponenseket, majd. Vegyünk néhány számszerű metodyresheniya ez az egyenlet. 1.4. Módszer egyszerű iteráció. Legyen egy egyenletet f (x) = 0, ahol f (x) -.