Szekvenciális rc-lánc
Tekintsük a sorozat RC-kör. sorozatából álló csatlakoztatott ellenállást és kondenzátort.
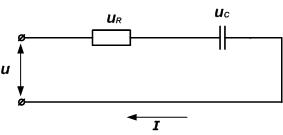
A kapocsfeszültsége az áramkör
Szerint a második törvénye Kirchhoff feszültség lehet ugyanaz, mint az összeg a feszültségesést ellenállás és a kondenzátor
Aztán az első kifejezés lehet átírni
A jelenlegi az áramkörben egyenlő
Behelyettesítve a fenti kifejezést, és integrálása, megkapjuk
Az ellenálláson eső feszültség egyenlő
A kondenzátor feszültsége
Mint látható az utolsó expressziós kondenzátor feszültsége lemaradt az aktuális szögben π / 2.
Reaktív (kapacitív) impedanciája a kondenzátor egyenlő
Csökkenő frekvencia a kondenzátor kapacitása megnő. Ha egy állandó áram egyenlő a végtelenségig, hiszen a frekvencia nulla.
A fáziseltolódás a sorozatban RC - áramkör lehet meghatározni, amelyet a képlet
Impedancia RC-kör
Tekintsük a példát a probléma megoldásának a RC-kör
Impedancia posledovatelnoyRC- lánc 24 ohm. A feszültség az ellenálláson 10 V, és az ellenállás 20 Ohm. Keresse C, Uc, U, I, shift fazφ. Vektor diagram.
Találunk átfolyó áram az ellenálláson. Mivel a vegyület a konzisztens, akkor az aktuális közös lesz az egész áramkört.
Ismerve a jelenlegi és az ellenállás az áramkör, megkapjuk feszültség
A kapacitív impedanciája a kondenzátor
Ismerve az ellenállás, kapacitás és feszültség találunk
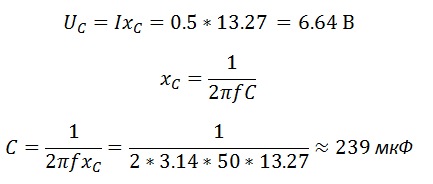
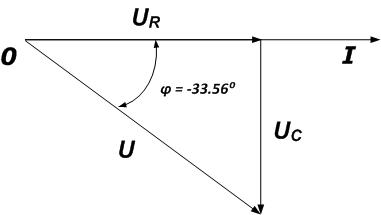
Készítünk egy vektor diagramján RC - lánc tehát tekinteni, hogy a kondenzátor feszültsége lemaradt az aktuális (ez nyilvánvaló a fáziseltolás jel).
Először is, a jelenlegi vektor lerakódik az áramkört, majd a feszültség az ellenálláson és a kondenzátor feszültsége. Ezután a teljes feszültség a vektort a összegeként vektorok kondenzátor feszültsége és az ellenállás.