feltételes valószínűség
A példákban korábban tárgyalt számított valószínűség elemi események. Felmerül a kérdés: hogyan lehet meghatározni a valószínűsége egy esemény, ha tudod, hogy néhány információt a megtörtént eseményekről vele? [1] A valószínűsége az esemény egy, a számítás, amely figyelembe veszi információ az esemény az úgynevezett feltételes V., és a továbbiakban, mint P (A | B).
A valószínűsége az esemény egy a feltétellel, hogy az esemény bekövetkezett B. egyenlő a valószínűsége esemény A és B osztva a valószínűsége az esemény:
Annak a valószínűsége, egy esemény, feltéve, hogy az esemény A jelentése a valószínűsége esemény A és B osztva a valószínűsége az esemény A:
ahol P (A és B) - valószínűsége esemény A és B P (A) - a valószínűsége az esemény A. P (B) - Annak a valószínűsége, egy esemény.
Letöltés egy megjegyzés Word vagy PDF
Tény, hogy a általános képletű (1) és (2) ez a gyors- feltételes valószínűség alapján kontingenciatábla. Tekintsük a példát, tárgyalt egy korábbi cikkben (ábra. 1). Tegyük fel, hogy tudjuk, ha néhány család fog vásárolni egy szélesvásznú TV. Mi a valószínűsége annak, hogy ez a család nagyon vesz egy TV-t?

Ábra. 1. Magatartás szélesvásznú TV vevők
Ebben az esetben ki kell számolnunk a valószínűsége P (vásárlás történt | vásárlás tervezett). Mivel tudjuk, hogy a család tervezi, hogy megvásárolja a minta tér nem tér el a 1000 családok, de csak azoknak, akik tervezik, hogy vesz egy szélesvásznú TV. 250 200 E családok valóban vásárolt TV-hez. Ezért a valószínűsége, hogy a család nagyon vesz egy szélesvásznú TV, ha a tervek ki lehet számítani a következő képlet segítségével:
P (vásárlás készül | vásárlás tervezett) = azoknak a családoknak, akik tervezik, és vettem egy szélesvásznú TV / háztartások száma tervezi, hogy vesz egy szélesvásznú TV = 200/250 = 0,8
Ez az eredmény ad a (2) képletű:
És ha az esemény az, hogy a család tervezi, hogy vásárol széles képernyős TV, és abban az esetben sem, - hogy valóban vásárolni. Behelyettesítve valós adatok, megkapjuk a képlet:
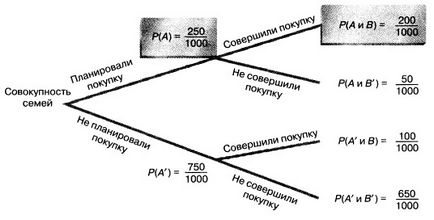
Ábra. 2. Döntési fa
Például, hogy kiszámítja a valószínűsége, hogy a család vesz egy szélesvásznú TV, ha azt tervezi, hogy ezt, meg a valószínűsége esemény ütemezve, és a vásárlás után. majd oszd el a valószínűsége az események tervezett vásárlást. Áttérve a döntési fa ábrán látható. 2, megkapjuk a következő (hasonló az előzőhöz) válasz:
A példában vásárol egy szélesvásznú TV a valószínűsége, hogy egy véletlenszerűen kiválasztott család vásárolt egy szélesvásznú TV, feltéve, hogy ő azt tervezte, hogy csináld, akkor 200/250 = 0,8. Emlékezzünk vissza, hogy a feltétel nélküli valószínűsége, hogy egy véletlenszerűen kiválasztott család vásárolt egy szélesvásznú TV, a 300/1000 = 0,3. Ez azt jelenti, hogy nagyon fontos következtetés. Előzetes információ, hogy a család tervezi, hogy megvásárolja, befolyásolja a valószínűsége legtöbb vásárlások. Más szóval, ez a két esemény független egymástól. Ezzel szemben a példában, vannak statisztikailag független esemény, a valószínűsége, amelyek függetlenek egymástól. Statisztikai függetlenségét fejezi ki az identitás: P (A | B) = P (A). ahol P (A | B) - a valószínűsége az esemény egy a feltétellel, hogy egy esemény történt B. P (A) - a feltétel nélküli valószínűsége az esemény A.
Megjegyezzük, hogy A és B események statisztikailag függetlenek egymástól akkor, ha P (A | B) = P (A). Ha a kontingencia-táblázat, amelynek mérete a 2 × 2, ez a feltétel teljesül, legalább egy fontos esemény az A és B igaz lesz bármilyen más kombináció. Példánkban a vásárlás tervezett események vásárlásról van szó, és nem statisztikailag függetlenek, mert az információt egy esemény befolyásolja a valószínűsége, hogy a többi.
Vegyünk egy példát, amely megmutatja, hogyan kell tesztelni a statisztikai függetlenség két esemény. Arra kérjük a 300 család, aki vásárolt egy szélesvásznú TV, függetlenül attól, hogy elégedett a vásárlást (3.). Annak meghatározása, hogy egy bizonyos fokú elégedettséget a vételi és az a fajta televíziós.
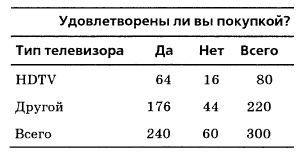
Ábra. 3. A jellemző adatokat fokú ügyfél-elégedettség szélesvásznú TV
Ezen adatok alapján,
P (vevő elégedett) = 240/300 = 0,80
Ezért a valószínűsége, hogy a vevő elégedett a vásárlás, és hogy a család megvette a HDTV-vel, egyenlő egymással, és ezek az események statisztikailag függetlenek, mert semmilyen módon nem kapcsolódik.
Szorzás szabálya valószínűség
A képlet a feltételes valószínűsége, lehetővé teszi, hogy meghatározzuk a valószínűsége, hogy a közös rendezvények A és B megoldása általános képletű (1)
viszonyított együttes valószínűsége P (A és B). Megkapjuk az általános szabály szorzata valószínűségek. Annak a valószínűsége, esemény A és B jelentése megegyezik a valószínűsége az esemény egy a feltétellel, hogy az esemény bekövetkezett B. szorozva a valószínűsége az esemény:
(3) P (A és B) = P (A | B) P * (B)
Tekintsük a példát, 80 család, akik megvették a szélesvásznú HDTV-vel (3.). A táblázat azt mutatja, hogy a 64 család elégedett a vásárlás, és 16 - nincs. Tegyük fel, hogy ezek közül véletlenszerűen kiválasztott két család. Határozzuk meg a valószínűsége, hogy mind a vevő elégedett lesz. A (3) képlet, kapjuk:
P (A és B) = P (A | B) * P (B)
És ha az esemény az, hogy a második család elégedett a vásárlás, és abban az esetben -, hogy az első család elégedett a vásárlást. Annak a valószínűsége, hogy az első család elégedett a vásárlás, annál 64/80. Ugyanakkor annak a valószínűsége, hogy a második család is elégedett a vásárlás, attól függően, hogy a válasz az első család. Ha az első család után a lekérdezés nem tér vissza a mintát (mintavétel nélkül csere), a válaszadók száma csökken 79. Mikor volt az első család elégedett a vásárlás, a valószínűsége annak, hogy a másik család is boldog lesz, a 63/79, mert csak 63 maradt a mintában családok elégedettek a vásárlást. Így, helyettesítve a (3) képlet specifikus adatok, megkapjuk a következő válasz:
P (A és B) = (63/79) (64/80) = 0,638.
Következésképpen a valószínűsége, hogy mindkét család elégedett a vásárlást, egyenlő 63,8%.
Tegyük fel, hogy kihallgatás után első család visszatér a mintában. Határozzuk meg a valószínűsége, hogy mindkét család boldog lesz a vásárlás. Ebben az esetben a valószínűsége, hogy mindkét család elégedett a vásárlást az azonos, és megegyezik a 64/80. Ezért a P (A és B) = (64/80) (64/80) = 0,64. Így a valószínűsége, hogy mindkét család elégedett a vásárlást, egyenlő 64,0%. Ez a példa azt mutatja, hogy a választás a második család nem függ a választott első. Így, helyett a (3) A feltételes valószínűség P (A | B), a valószínűsége, P (A). megkapjuk a képlet megszorozzuk a valószínűsége független események.
A szabály szorzata valószínűségek független események. Ha A és B események statisztikailag független, a valószínűsége az események A és B jelentése megegyezik a valószínűsége egy esemény szorozva a valószínűsége A. Az esemény.
Ha ezt a szabályt tartja az A és B események azt jelenti, hogy statisztikailag független. Így kétféleképpen határozza meg a statisztikai függetlenség két esemény:
- A és B események statisztikailag független egymástól, ha, és csak akkor, ha a P (A | B) = P (A).
- A és B események statisztikailag független egymástól, ha, és csak akkor, ha a P (A és B) = P (A) P (B).
Ha a vészhelyzeti asztal, amelynek mérete a 2 × 2, az egyik ilyen feltételek egyike teljesül legalább egy kombinációs események A és B igaz lesz bármilyen más kombináció.
A feltétel nélküli valószínűsége egy elemi esemény
ahol B1 eseményeket. B2. ... Bk kölcsönösen kizárják egymást, és kimerítő.
Mi alkalmazásának illusztrálására e képletnek, például az 1. ábra. A képlet (5), kapjuk:
ahol P (A) - a valószínűsége, hogy a tervezett vásárlás, P (B1) - annak a valószínűsége, hogy a vásárlás létrejön, P (B2) - annak a valószínűsége, hogy a vásárlás nem készül.
A feltételes valószínűsége az esemény lehetővé teszi az információk arról, hogy mi történt néhány más esemény. Ez a megközelítés lehet használni, hogy frissítse a valószínűségek alapján újonnan érkezett információ, és kiszámításának a valószínűsége, hogy a megfigyelt hatás következtében néhány konkrét oka. tisztázza az eljárás ezen valószínűségek hívják Bayes tétel. Ez volt az első által kifejlesztett Thomas Bayes a 18. században.
Tegyük fel, hogy a vállalat a fent említett, kutatjuk a piacon egy új TV modell szerint. A múltban, 40% -a TV-készülékek által létrehozott cég, a siker, és 60% nem kapta meg a felismerés modellek. Mielőtt be a kibocsátás egy új modell, a marketingesek megvizsgálja a piaci és elfog a kereslet. A múltban, a siker 80% -a modellek kaptak elismerést, megjósolt előre, ugyanakkor 30% kedvező előrejelzések nem voltak megfelelőek. Az új modell a marketing osztály adta kedvező prognózist. Mi a valószínűsége annak, hogy az új TV lesz kereslet?
Bayes-tétel lehet következtetni meghatározása feltételes valószínűség (1) és (2). Kiszámításához a valószínűsége P (B | A), hogy a (2) képletű:
és helyett helyett P (A és B), az érték a (3) képletű:
P (A és B) = P (A | B) * P (B)
Behelyettesítve a P (A) általános képletű (5), kapjuk Bayes tétel:
ahol B1 eseményeket. B2. ... Bk kölcsönösen kizárják egymást, és kimerítő.
Bemutatjuk a következő jelöléseket: S esetén - a tv-kereslet. Esemény S „- a TV nem a kereslet. Esemény F - kedvező prognózist. Esemény F „- a rossz prognózist. Tegyük fel, hogy P (S) = 0,4, P (S ') = 0,6, P (F | S) = 0,8, P (F | S') = 0,3. Alkalmazása Bayes-tétel kapjuk:
Annak a valószínűsége, hogy igény van egy új modell a TV, amennyiben kedvező prognózist 0.64. Így a valószínűsége kereslet hiánya, feltéve, kedvező prognózist 1-0,64 = 0,36. A számítási folyamat ábrán látható. 4.

Ábra. 4. (a) A számítást a Bayes képlet megbecsülni a valószínűsége televíziók kereslet; (B) a döntési fát a tanulmány a kereslet az új TV modell
Vegyünk egy példát alkalmazása Bayes-tétel az orvosi diagnózis. Annak a valószínűsége, hogy egy személy szenved egy adott betegség, egyenlő 0,03. Orvosi vizsgálat lehetővé teszi annak ellenőrzését, hogy ez így van. Ha valaki nagyon beteg, a valószínűsége a pontos diagnózis (arra hivatkozva, hogy valaki beteg, ő tényleg beteg) egyenlő 0,9. Ha egy személy egészséges, annak valószínűsége, hogy a téves pozitív diagnózis (azt állítva, hogy a beteg ember, amikor egészséges) 0,02. Tegyük fel, hogy egy orvosi vizsgálat pozitív eredményt. Mi a valószínűsége, hogy egy személy valóban beteg? Mi a valószínűsége, hogy a pontos diagnózis?
Bemutatjuk a következő jelöléseket: Event D - valaki beteg. Esemény D „- az a személy egészséges. Esemény T - pozitív diagnózist. Esemény T „- a diagnózis negatív. Tól feladat helyzetben azt jelenti, hogy a P (D) = 0,03, P (D ') = 0,97, P (T | D) = 0,90, P (T | D') = 0,02. Képlet alkalmazásával (6), kapjuk:
Annak valószínűsége, hogy egy pozitív diagnózis egy személy valóban beteg, egyenlő 0,582 (lásd. Ábrát is. 5.). Megjegyezzük, hogy a nevező képletű Bayes valószínűsége pozitív diagnózis, azaz 0,0464.
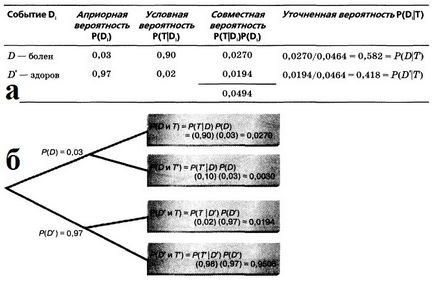
Ábra. 5. (a) A számítást a Bayes képlet becslésére pontosságának orvosi diagnózis; (B) a döntési fa értékelésekor pontosságát orvosi diagnózis
Ön is érdekelt: