Az egyetemes tömegvonzás törvénye
Szerint a Newton második törvénye mozgás változásokat okozhat, azaz a. E. Az ok a gyorsulás szervek olyan erő. A szerelők tartják erők különböző fizikai jellegű. Sok mechanikai jelenségek és folyamatok határozzák meg a gravitáció hatására.
A gravitáció törvénye fedezte fel Newton 1682-ben. Vissza 1665-ben a 23 éves Newton azt javasolta, hogy a gazdaság erői Hold pályáján, ugyanolyan jellegű, mint az erők, melyek hatására az alma a földre esik. Szerint a hipotézis, az összes szervek a világegyetem, vonzó- (gravitációs erő), irányított összekötő egyenes mentén a tömegközéppontjai (ábra. 1.10.1). A koncepció a súlypont szigorúan meghatározott § 1.23. A test formájában teszi egy homogén massza a labda középpontja egybeesik a központja a labdát.
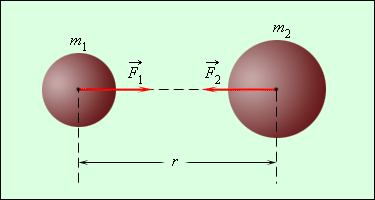
A gravitációs vonzóerő szervek között.
Az ezt követő években Newton próbált találni a természetes magyarázata jogszabályok bolygó mozgás (lásd. §1.24), nyilvános csillagász J. Kepler a korai XVII században, és kvantitatív kifejezést a nehézségi erő. Tudva, hogy a bolygók, Newton akarta meghatározni, hogy mi erők hatnak rájuk. Ez az út az úgynevezett inverz feladat a mechanika. Ha a fő célja a mechanika, hogy meghatározza a koordinátákat a test ismert tömegű és sebessége bármely időpontban az ismert ható erők a test, és adja meg a kezdeti feltételeket (közvetlen mechanikai probléma), ha megoldása az inverz probléma meg kell határoznia a testre ható erők, ha ismeretes, hogyan mozog. A megoldás erre a problémára vezetett a felfedezés Newton-féle gravitációs törvény.
Minden test vonzzák egymást erővel egyenesen arányos a tömegek és fordítottan arányos a távolság négyzetével köztük:
Az arányossági tényező G ugyanaz az összes szervek jellegű. Ez az úgynevezett gravitációs állandó
G = 6,67 · 10 -11 Nm 2 / kg 2 (SI).
Sok jelenség a természetben magyarázzák a gravitáció hatására erők. A mozgalom a bolygó a Naprendszerben, mesterséges holdak, röppálya a ballisztikus rakéták, a mozgás szervek mellett a Föld felszínén - mindegyiket lehet magyarázni alapján az egyetemes tömegvonzás törvénye és a törvények dinamikáját.
Egyik megnyilvánulása az egyetemes tömegvonzás erő a gravitációs erő. Az úgynevezett gravitációs testek közelében a Föld felszínét. Ha M - tömege a Föld, RG - annak sugara, m - test tömege, a gravitációs erő egyenlő
ahol g - a nehézségi gyorsulás a Föld felszínén:
A gravitációs erő irányul a Föld középpontja. A más erők hiányában a test szabadon esik a Földre gyorsulással szabadesés. Az átlagos értéke a gravitációs gyorsulás különböző pontokat a föld felület 9,81 m / s 2. ismeretében a gravitációs gyorsulás, és sugara a Föld (rg = 6,38 × 10 6 m) tömegének kiszámításához M a Föld:
Amikor a távolság a a Föld felszínén gravitációs erő a föld és a nehézségi gyorsulás megváltoznak fordítottan arányos a távolság négyzetével R a Föld középpontjába. Ábra. 1.10.2 változását szemlélteti a gravitációs erő hat űrhajós egy űrhajó annak távolsága a Földtől. Az az erő, amely az űrhajós vonzódik a Föld a felszín közelében, feltételezzük, hogy 700 N.
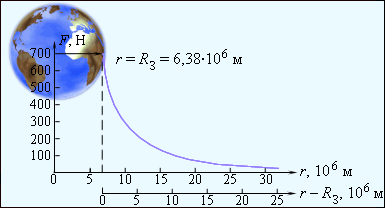
Megváltoztatása a gravitációs erő hat a űrhajós a távolság a Föld
Egy példa a rendszer két kölcsönható testek szolgálhat a Föld-Hold rendszert. Moon bizonyos távolságra a föld rL = 3,84 × 10 6 m. Ez a távolság körülbelül 60-szerese a Föld sugara RG. Következésképpen a gravitációs gyorsulás al. miatt a vonzás a föld a pályán a Hold
Ilyen gyorsulás közepe felé a Föld, a Hold mozog a pályáján. Következésképpen ez a gyorsulás a centripetális gyorsulás. Meg lehet kiszámítani a kinematikai képlet centripetális gyorsulás (lásd §1.6.):
ahol T = 27,3 nap - a keringési idejének a Hold a Föld körül. A véletlen eredményeinek végzett számítások különböző módon megerősíti azt a feltételezést az egységes természet Newton erő tartja a Hold körüli pályára, és a gravitáció.
Saját gravitációs mező a Hold határozza meg a gyorsulás szabadesés dl felületén. A tömege a hold 81-szer kisebb, mint a Föld, és sugara körülbelül 3,7-szer kisebb, mint a sugara a Föld. Ezért, a gyorsulás a dl által adott kifejezést:
Az ilyen alacsony gravitáció az űrhajósok, akik landolt a Holdon. Egy ember ilyen körülmények között is, hogy hatalmas ugrásokkal. Például, ha egy személy a Földön pattog a magassága 1 m, a Holdon, nem tudott ugrani a magassága 6 m.
Nézzük a kérdést, mesterséges föld műholdak. Mesterséges műholdak mozgása kívül a Föld légkörébe, és ezek csak a gravitációs erő a Földön. Attól függően, hogy a kezdeti pályája sebességét külső test különböző lehet. Itt most csak az esetben, ha mozgás a műhold egy kör alakú pályára a Föld körül. Ezek a műholdak repülni magasságban 200-300 km-re, akkor feltételezhető, mintegy a távolság a Föld középpontjába egyenlő sugarú rg. Ezután a műholdas centripetális gyorsulás visznek fel, a gravitációs erők, megközelítőleg egyenlő a gyorsulás szabadesés g. Jelöljük a sebessége a műhold Föld körüli pályára keresztül υ1. Ez a sebesség az úgynevezett első kozmikus sebességet. Használata kinematikus képlet a centripetális gyorsulás. kapjuk:
Vezetés olyan sebességgel, a műhold kering a Föld lenne egy időben
Tény, hogy a keringési idejének a műhold egy kör alakú pályán, közel a Föld felszínét kissé magasabb, mint a megadott érték közötti különbségek miatt a tényleges méretét a pálya és a Föld sugara.
A mozgás a műhold lehet tekinteni, mint a szabadesés mozgás, mint a lövedékek, vagy ballisztikus rakéták. Az egyetlen különbség az, hogy a sebesség a műhold olyan nagy, hogy a görbületi sugara útját egyenlő a Föld sugara.
A műholdak mozgó körpályák jelentős távolságra a föld, a gravitáció csökken fordítottan négyzetével r sugarú a pálya. υ az a sebesség, a műhold a feltétel
Így a nagy pályák műholdak mozgás sebessége kisebb, mint az alacsony Föld körüli pályán.
A T időszakban a referencia műhold
Itt T1 - időszakban a műhold alacsony Föld körüli pályán. orbitális időszakban növekszik a sugara a pályára. Könnyen kiszámítható, hogy a pálya sugara r egyenlő körülbelül 6,6 rg. időszakban a műhold lesz 24 órán belül. A műhold orbitális időszakban fut a gépen az egyenlítőtől, még lógni bizonyos ponton a Föld felszínét. Az ilyen műholdat használnak az űrben rádiós rendszerek. A sugarú körpályán r = 6,6 RG úgynevezett geostacionárius.