magnetomechanikai jelenségek
,
Ismét kaptunk egy homogén másodrendű differenciálegyenlet.
Ez az egyenlet nem különbözik attól, amit kaptunk a tavaszi inga az előző részben. Ezért a döntés ugyanolyan alakú :, hol.
Ez azt jelenti, hogy csillapodó rezgéseinek előfordulhat a rezonáns áramkör energiaveszteséget.
7.3. A jellemzői csillapodó rezgéseinek
A megoldás a differenciálegyenlet azt mutatja, hogy az amplitúdó csillapodó rezgéseinek csökken a törvény idővel. Minél nagyobb a hányados b, annál gyorsabb a rezgésamplitúdót csökken. Ezért nevezik a csillapítási tényezője.
Mivel amennyiben rezgések csillapodnak gyorsabban, mint a nagyobb súrlódási együttható R, és minél kisebb a terhelés az oszcilláló m tömegű.
Ez a következtetés egészen érthető - minél több súrlódás, amely megakadályozza, hogy a mozgás, annál gyorsabb a pre-szeres oszciiiáiómozgásban egy igazi oszcillátor. Csökkenti a tömeg-shenie azt jelenti, hogy csökkent ellátása a kinetikus energia az oszcillátor, és így egyenlő súrlódási energia hamar elfogy legyőzni azt.
Jelölő szimbólum t idő, amelyre a rezgési amplitúdója faktorral csökken e, akkor m. E. Bt = 1 és.
Így, b a reciproka az időt, amely az amplitúdója faktorral csökken e.
A t idő az úgynevezett relaxációs idő
Mivel a csillapítási jellemzők is használják logaritmikus csökkentéshez
,
ahol A (t) - rezgési amplitúdó egy bizonyos ponton t; A (t + T) - rezgési amplitúdó után egy periódusának csillapított rezgésnek.
Ebből kapcsolatban az következik, hogy l = BT.
Megvalósíthatósága az ilyen jellemzők látható, a következő.
Mivel az L = BT. és b = 1 / T, eddig. De T - az az idő, amelyben az egyik zajlik a rezonanciát és a t - idő, ameddig nem lesz, általában több oszcilláció *.
,
ahol Nc - rezgések száma, amely alatt a amplitúdója faktorral csökken e.
Így b és l gyengítő tulajdonságok, amelyek kiegészítik egymást: b megmutatja, milyen gyorsan csillapodó rezgések de nem tartalmaz információt a rezgések száma; l azt is mutatja, hogy mennyi a rezgés amplitúdója faktorral csökken e, de semmit nem mond az időt, amely nem lesz a csökkenés.
A megoldások a differenciálegyenlet is jelenti, hogy a frekvencia a csillapított rezgési frekvenciája w kisebb, mint ideális WO inga oszcilláció. .
Ciklikus gyakorisága w és WO kapcsolódó következőképpen. Tegyük fel, inga végez csillapodó rezgések frekvencia w; Ha megszabadulni a súrlódás, elvégzi harmonikus oszcilláció frekvenciája WO.
Mert ahol r - súrlódási együttható növekvő súrlódási csillapított rezgési frekvenciája csökken.
Ingadozások elkövetett tavaszi inga súrlódás, nem harmonikus.
* Ennek során az amplitúdó a rezgések pontosan és szeres faktorral csökken, e.
Azt is nem, és időszakos. Azonban a fizika elterjedt az úgynevezett időszak csillapodó rezgések; míg az T jelenti az időt, amely alatt egy oszcilláló zajlik.
7.4. kritikus csillapítás
Kvalitatív alapon c. 7 kimutatták, hogy kellően nagy súrlódási ingadozásokat lehetetlenné válik. Származó egyensúlyi helyzet vibrációs rendszer egyszerűen visszaadja.
Ez a mód a valós oszcilláló rendszer akkor jelentkezik, ha b okot, hogy a körülmények, és nyilvánvaló lesz.
Ebben az esetben, a megoldás a differenciál-differenciálegyenlet a következő alakban:
,
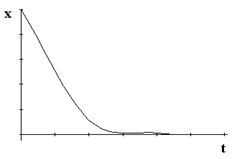
t. e. x függ az időben a ex-exponenciális, nincs oszcilláció. A rendszer, amely származik az egyensúlyi helyzet, nagyon lassan visszatér (lásd. Ábra).
Csillapítása, amely az úgynevezett kritikus. Ezzel (és nagy) csillapító oszcilláció a rendszerben lehetetlen.