Hogyan lehet megoldani a problémákat kapcsolatos funkciók és grafikonok
lecke témában. „Hogyan alakítsunk egy levelezés között a grafikonok a funkciók és a jelei a és b együtthatók”.
1. lecke: „Hogyan alakítsunk egy levelezés között a grafikonok a funkciók és az együtthatók előjelei a és b.”
2. lecke „hogyan kell létrehozni a levelezés a grafikonok a funkciók és az együtthatók előjelei és c”
3. lecke: „Hogyan lehet megtalálni a koefficiens értéke és a grafikon a másodfokú függvény.”
4. lecke: „Hogyan lehet megtalálni az érték a b tényező az ütemezésnek megfelelően a másodfokú függvény.”
Ismétlés.
- A funkció az űrlap y = a x 2 + b x + c c. ahol a ≠ 0 nevezzük másodfokú függvényt.
Az egyenletben a másodfokú függvény
egy első együttható,
második tényező b,
tag -mentes
A grafikon a másodfokú függvény másodfokú parabola.
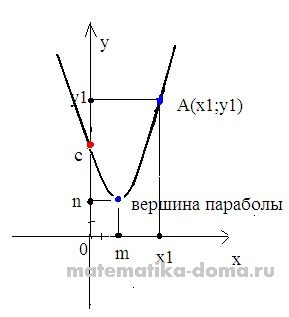
Hogyan állapítható meg, a jel egy együtthatóval.
- Egy függvény az y = x 2, ahol az ágak vannak irányítva felfelé formában van:
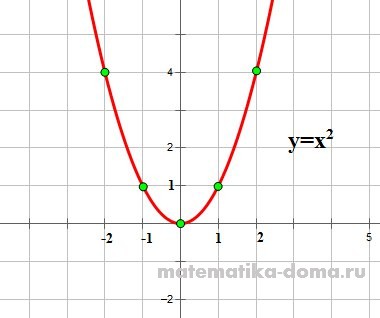
- Egy függvény y = -x 2, ahol az ágak lefelé irányulnak formában van:
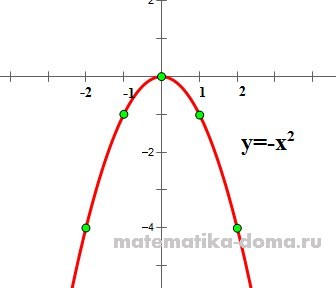
- Ha az első tényező a> 0, akkor a parabola ága felfelé irányuljon.
- Ha az első együttható <0, то ветви параболы направлены вниз.
Hogyan állapítható meg, a jel az együttható b.
Mint látható jele az együttható meghatározásához a menetrend nem nehéz. Ugyanilyen nehéz meghatározni a megjelölés az együttható b.
Erre ott van a következő szabály, amely hibátlanul működik.
- Ha a> 0 és b> 0, a parabola csúcsa található a bal felét
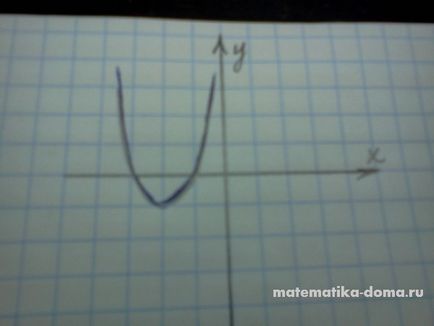
- Ha a> 0 és b <0, то вершина параболы расположена в правой полуплоскости
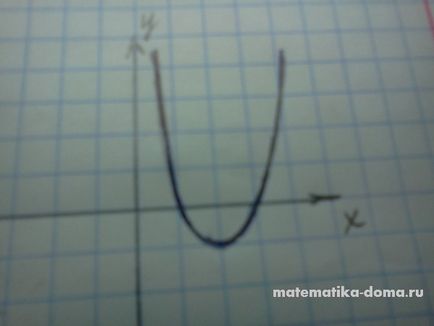
- Ha egy <0 и b>0, a csúcsa a parabola található a jobb fele
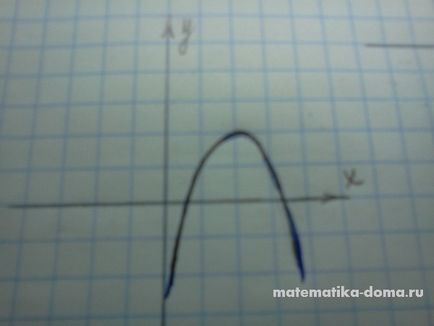
- Ha egy <0 и b <0, то вершина параболы расположена в левой полуплоскости
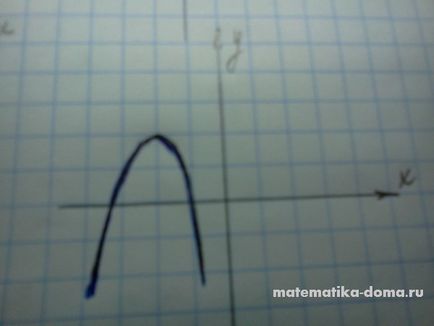
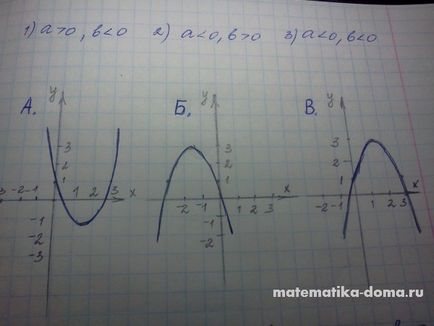
Az ábra azt mutatja, grafikonok a funkciók y = ax 2 + bx + c. Közötti kapcsolatot határozzák meg a grafikonok a funkciók és jelzi a és b együtthatók.
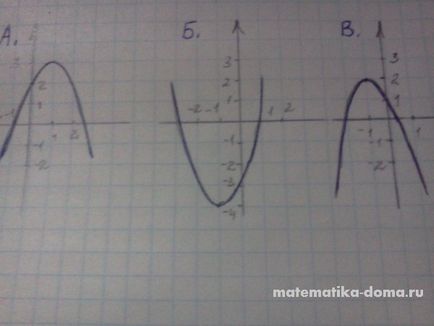
1) a> 0, b> 0 2) egy<0,b<0 3)a<0,b>0
Ábra A - a parabola ágai a lefelé. ez azt jelenti,<0, вершина параболы расположена в правой полуплоскости, значит b>0. Ez megfelel a 3. ábrára.
Ris.B - parabola ága felfelé irányított, azt jelenti, a> 0, a csúcsa a parabola található a bal fél-sík, majd a b> 0. Ez a szám megfelel az 1.
A fényképek B - a parabola szára lefelé, majd<0, вершина параболы расположена в левой полуплоскости, значит b<0. Этот рисунок соответствует 2.
Önálló munkát.
Téma: Hogyan lehet létrehozni egy levelezés között a grafikonok a funkciók és a jelei a és b együtthatók”.
És most válassza ki a saját tevékenységi 5 Opciók 7. és 12. A szükséges ismereteket, hogy megoldja danogo munkát már van.
Az ábra azt mutatja, grafikonok a funkciók y = ax 2 + bx + c. Közötti kapcsolatot határozzák meg a grafikonok a funkciók és jelzi a és b együtthatók.
Az ábra azt mutatja, grafikonok a funkciók y = ax 2 + bx + c. Közötti kapcsolatot határozzák meg a grafikonok a funkciók és jelzi a és b együtthatók.
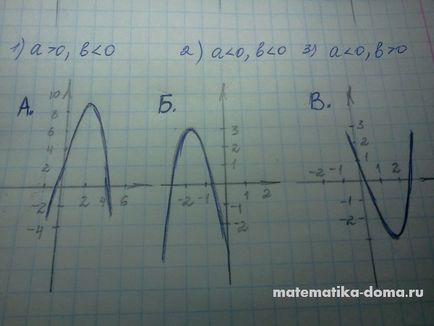
A teszt a döntést, lásd. A válaszok az alábbiakban.