Előtt és után a radián
I. problémák és okaik
A fő feladat a tanár - tanítani a diákokat, hogy úgy gondolja, ezzel a GEF. Föld megvilágított a nap, és az a személy - a tudás. „A tudás - a legkiválóbb tartásához. Minden vágynak rá, nagyon jól, hogy nem jön „- Abu Rayhan Beruni.
A következő feladat -sdacha végzős vizsga. „A tanulmány trigonometria nem a” átlagos elmék”, különben is, ez unalmas és haszontalan tevékenység. Nem számításához tanítás, mint a vizsga tesztek kínált egyetlen egyenlet 2 pontot „- hisz diplomások. Kifejtsék véleményüket a vizsga, azok befolyásolják társaik. Igyekszünk, hogy figyelembe veszi a valós helyzetet az iskolában.
Szüksége trigonometria és származéka, a motiváció, - a fő oka céljaival összhangban és érdekeit a sikeres tanulmányi oktatási anyag. A kiindulási pont a nyelvi kérdés formális matematikai nyelv - a megértés hiánya egyediségét a matematikai jel, szimbólum, stb .. Trigonometry természetesen a morzsákat szórt 1 Grade 9. és nem járul hozzá a fejlesztési hallgató myshlneniya .. A tanítvány tudja „mit, hol és mikor” vizsgálat alatt nagyon fontos és elengedhetetlen, de ez a „távoli messze» motiválja jelenleg tetteit. Adatátvitel algebra és geometria a grade 6-7 csökkentette az érdeklődést a vizsgált anyag (megváltoztatni a kor). A program írt 7 osztály „hogy képes képviselni a pontok száma a koordináta-tengely”, és nem írt, hogy egy körön „számítások elvégzésére képletek szerint” a hangsúly a képlet a kör és a kör (szükséges), hozzátéve, a szétválás a kerülete a 12; 6; 4; 8. 2 rész, aláírásával a ív hossza, ha R = 1. Periodikus függvények az általános iskolában nem tanulnak, és a diplomások 9 osztály nem kap ismereteket a témában teljes térfogata. Vizsgálni trigonometry 10 tanóra alatt kiosztott 56% a tananyag. Mivel az érték a trigonometria, utalni kell értékelni C1 4 pont. Mindenben tudnunk kell, mikor kell abbahagyni. Akik tetteikkel azt mutatjuk be, a hiábavalóság diákok trigonometria. Közben Thomas Paine, című könyvében: "The Age of Reason" (1794) nevű trigonometria, "a lélek a tudomány."
II. Az ok a trigonometria
Fractal - ez az, amit sokan mondják manapság. Fractal - ez a szám. egy bizonyos részét, amely ismétlődik, megváltozott méretű. ez elvéből következik önhasolóság. Részei fraktálok, mint az egész szám. Matematika tanulmányozza a természet formái. amelyben az ugyanezen törvény intézkedéseket. Ennek egyik oka a kialakulásának trigonometria van”... a képtelenség, hogy alakját írja le a felhők, hegyek vagy fák. Felhők - ez nem egy gömb. hegyek - nem sarkok „- írta alapító fraktálok Benoit Mandelbrot elmélete. Keresztül egyenletek és tételek megoldani a problémát leírása íves felületek és vonalak.
III. görbület korrekciós
Nézd meg a tenyér. Mit látunk? Ha feltételezzük, hogy az ujjak egyenesen, és vigye a sugarak származó tenyér hold kidudorodás, feltételezhetjük, hogy alkotnak szögek 0 °; 30 °; 45 °; 60 °; 90 °. Pinky iránya megfelel a kezdődő hivatkozási szögek és a hüvelykujj - 90 °.
Nézzük meg a hegyet egy matematikai szempontból. Mit látunk?
Ha vesszük hajlított hegy határán egyenes vonalak, a lejtőn a hegy a bázis szöget. Sinus lefordították orosz nyelven azt jelenti görbület, hajlítás és sinα =. Ott kezdődött a kapcsolat a másik lábát, hogy az átfogó és a derékszögű háromszög, az épület egy bizonyos kapcsolatban lábat az átfogója, megkapjuk a kívánt szöget. Hegység és a lépcső meredek, sekély, de ez attól függ, hogy a szöget.
c) Az architektúra a részleteket formájában az emberi test csontjait
A fő épületben formájában vannak geometriai szilárd. Gyakori, hogy az összes alkotás Antoni Gaudi volt, a megdicsőülés a természet, ahol minden harmóniában. Én nézett szemével egy építész Gaudí az emberi test, amely számos anatómiai részletek nincsenek éles sarkok, és őket az építészet. Gyűlölte a sarkok és éles egyenes vonalak a geometria. Úgy vélte, hogy az egyenes által teremtett ember, a természet bemutatott egy görbe vonal, és a kör - egy isten. A felület görbülete egyenlet által definiált Z = k x sin. Megváltoztatásával néhány tényező az egyenletben, lehetséges, hogy szinte végtelen lehetőségeket az eredeti kép.
Lehetővé vált, hogy rögzíti a szívverés ritmusát és a rezgések a föld.
IV. Előtt és után a radián
Euler létre trigonometria, mint tudomány a funkciókat. Tagja az elképzelést, figyelembe véve a trigonometrikus függvények, mint arányok a megfelelő szegmensek a kör sugarát, hogy van, mint ez a szám megengedett negatív szögek és szöge nagyobb, mint 360 ° C.
Annak megállapítására, a funkciók egy levelezés között a számok támaszkodva vizuális képeket. Van egy hivatalossá szigorú érvek hosszasan egységek beadott 1 radián. ami nem mondható el a szokásos hosszúságú darabot. A „rad” jelent meg a 18. században. Radiánban a szög az az előnye, mint a szokásos mérési szög fokban, hogy a természetes.
a) A hossz aránya felemelni útvonal: NM. AN = BC. AB = sina.
c) Meg kell választani az intézkedést. Egy ilyen intézkedés az, hogy az R és meg kell tenni, mint 1.
d) Ha a piros kört vág a ponton A és szakaszon, megkapjuk otrzok AB ahol C = C - kerülete. Átmérő késik több mint 3-szor.
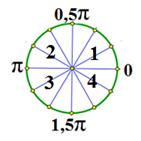
Point, a kerület mentén húzódik n-szer, teszi 2πRn úthossz, n Je Z és R = 1, akkor a ritmust megismételjük mer hosszúságú 2π. Valódi vonal lesz egyenlő n-nel numerikus körökben 2πRn, ahol R = 1, azaz a (-∞; ∞) = 2πn, ahol n Je Z.
V. Az egyenlet periodikus függvények és azok grafikonok
Vegyünk egy pontot a koordináta síkon (x, y) és ΔOVS konstrukció. Rajzoljunk egy kör közepén a O és a sugara OB = 1. Mivel a B pont fekszik a kör, kapjuk a (t), ahol t-ᴗ érték VC az értéke radiánban ے BOC. A definíció szerint a szinusz és koszinusz van sint =. költség =. Az arány az átfogója a lábak függ a hegyesszög t. Ha R = 1 imee: Sint = BC = y, költség = OS = x, azaz X = költség; y = sint. Az érv t, tєR. Térjünk át a szokásostól: y = cosh; y = Sinh, hєR.
1. A grafikon egy periodikus függvény y = sinx, hєR
2. Szűk megoldásában egyenletek
- Megtalálni a koordináta pont a kör tartozó koordinátasík.
- Tájékozódás osztály kör 2; 4; 6; 8 és 12 egyenlő részre. Értékelése elosztjuk az ár.
- A kiválasztás megoldások az intervallumon.
VI. A szimulációs program számára a webes tudás ékezetes
„Amikor az emberek nem tanulnak, mit kell gondolni, és mit kell gondolni, majd eltűnik mindenféle félreértések” - G.Lihtenberg.