Az egyenletek megoldása tartalmazó modul jelet
Komsomolskaya VAGY №5 I - III szakaszok
SOLUTIONS, hogy tartalmazza a modul MARK
modul egyenletek megoldás nehézségeket okoz a diákok.
Elemezve a munka felvételi, meg kell jegyezni, hogy nagyon gyakran állásajánlatot a modulokat. Annak érdekében, hogy a diákok megtanulják, hogyan lehet megoldani egyenletek modulok kínált ezt az anyagot.
Egyenletek modul csoportra oszthatók módszere szerint oldatuk. Mindegyik csoport kap elméleti anyag. megoldásához szükséges egyenleteket a csoport.
Vannak megoldások az egyenletek az egyes csoportok és az egyes egyenletek algoritmus megoldásuk, amely lehetővé teszi a diákok az önképzésre.
Ezt az anyagot fel lehet használni az osztályban, amikor dolgozik csoportosan és egyénileg egyaránt az osztályban, és a házi feladat.
Célja a diákok az osztályok törlődik.
Tartalmazza a változó a modulus
Egyszerű egyenlet a modul a forma (1) egyenlet
ahol - bizonyos funkciók.
Annak érdekében, hogy megoldja ezt az egyenletet, akkor először meg kell találni az összes egyenlet megoldásai = tartozó set, majd oldja meg az egyenletet = a sor; az unió a talált megoldásokat van a készlet minden oldatok (1) egyenlet. Más szóval, (1) egyenlet egyenértékű a aggregált rendszerek
Az eredeti egyenlet egyenértékű a több rendszerek:
Válasz. - 3; - 2; 2; 3.
Egyenlet a forma egyenértékű a aggregált rendszer (lehet megoldani két módon)
Ez az egyenlet egyenértékű a több rendszerek:
Ez nem felel meg a feltételnek, ezért a rendszer a megoldás.
Ez nem felel meg a feltételnek, ezért a második rendszer van egy megoldás.
Egyenlete formájában, ahol - bizonyos funkciók egyenértékű az egyesített rendszerek
Ez az egyenlet egyenértékű a kombinációja két rendszer:
1). A rendszer nem megoldás.
Megoldásában a egyenletek, ahol a modulus egy expressziós tartalmazó modul először meg kell szabadítani a belső modulok, majd ezen egyenletek felfedi a fennmaradó modulok.
Ez az egyenlet ekvivalens az összesített a két rendszer
azaz az összessége rendszerek
A második rendszer nem megoldás. Az első rendszer ekvivalens az alábbi két rendszer:
5. Az eljárás bontani időközönként. Az egyenlet a forma (2)
Oldani a rések (vagy a módszer a felosztás intervallumok). Ehhez először megtalálja a pontokat, ahol a
Ezek a pontok osztják tartományban megengedett értékek (2) egyenlet időközönként, melyek mindegyikében az összes tárolt jel funkció (feltételezve, hogy a jel az egyes modulok az említett rés). Ezután mozgassa a (2) egyenlet és több rendszerek, a modul nem tartalmazó karaktereket.
18. Keresse meg a gyökere az egyenlet kielégítő egyenlőtlenség.
Válaszokat és megoldásokat.
2. A módszer bontani időközönként.
A modul, amely tartalmazza a paramétereket.
1. Minden egyes paraméter értékét megtalálják a számát gyökerei az egyenlet.
Határozat. Az egyenlet formájában, mivel nem gyöke egyenlet. Száma gyökerei az egyenlet számának felel meg a metszéspontja a grafikon és a vonal. Készítünk egy függvény grafikonját, amely két részből áll:
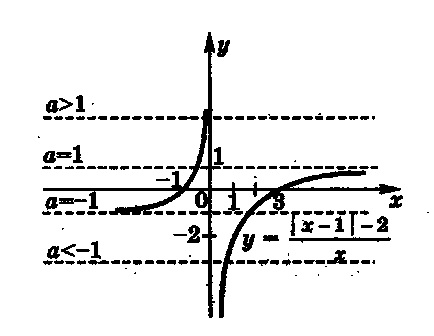
Az ábra azt mutatja, hogy a
egyetlen metszéspontja, ami azt jelenti, hogy egyetlen gyökér;
ha két metszéspontot, ami azt jelenti, hogy az eredeti egyenletnek két gyöke;
alatt - az egyik határátkelő, ami azt jelenti, hogy az egyenletnek csak egy gyökér.
Továbbra is látni, hogy mennyi a gyökerei az eredeti egyenlet van, és.
Tegyük fel, akkor az eredeti egyenlet. Határozzuk meg a számát gyökerei az egyenlet.
Tegyük fel, akkor van a következő egyenletet:
Válasz: Ha az egyenletnek csak egy gyökér;
ha az egyenletnek két gyöke;
ha az egyenletnek egy egyedülálló megoldás.
2. Minden paraméter értékét megtalálják a számát gyökerei az egyenlet.
Határozat. Írja át az egyenletet formájában.
Mi határozza meg a pontok számát a kereszteződésekben a grafikon, hogy megoldja a problémát, és. Építünk a függvény grafikonját
amely két részből áll:
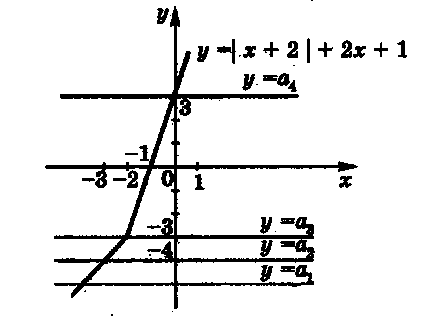
Az ábra azt mutatja, hogy minden értéke az eredeti egyenletnek egy gyökér.
A: minden értéke az eredeti egyenletnek egy gyökér.
3. milyen értékeket egy paraméter egyenlet
Ez legalább egy megoldás?
Határozat. Podmodulnaya funkció
Ha, akkor, mivel, ahol az egyenlőség csak úgy érhető el, ha az.
Ha tehát az egyenlőség elérése csak.
Tehát, mindenki számára. Mivel, a (1) egyenlet egyenértékű a rendszert, és csak akkor, ha a paraméter értékek által talált az eredeti egyenlet van egy megoldás, ti.
1. Minden egyes paraméter értékét megtalálják a számát gyökerei az egyenlet
2. Minden paraméter értékét megtalálják a számát gyökerei az egyenlet
3. milyen értékeket az egyenletnek van legalább egy megoldás?
1. Ha az egyenletnek egyedülálló gyökér;
ha az egyenletnek két gyöke.
2. bármilyen értéket az egyenlet van egy egyedi gyökér.