Előadások torziós hengeres rudak
Torziós hengeres rudak.
Tekintsünk egy hengeres rúd (1), amely oldalfelületek mentes terhelés, és csatolja a homlokfelületek pillanatok vannak irányítva középvonala mentén a rúd. Tengely mentén irányul tengelye a rúd.
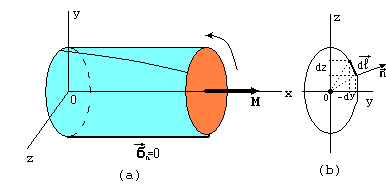
1. ábra torziós nyomaték. Oldalsó felületén erők nem hatnak: feszültség vektor nulla.
A következő egyenletek egyensúly a rugalmas közeg hiányában súlyerő:
Egyenletek (1) kell megoldani homogén (feszültség vektor nulla), a peremfeltételek oldalsó felületén, ahol a normál vektor
A végfelülete a kapott vektort erők nullának kell lennie, és a fő szempont van megadva, és csak egy komponense a tengelyen. Ezért, hogy megkapjuk a komponenseket a kapott vektort
A komponenseket a kapott pillanatban vektort a feltétel
vagy három skalár
Tegyük fel, hogy a normális része a rúd sima és forgatjuk csak szöge arányos a köztük lévő távolság
Nulla törzseket és feszültségek:
Megjegyezzük, hogy a feszültség azonos kielégítik az egyensúlyi egyenletek (1), és az utolsó két peremfeltételek (1) és azok helyettesítése az első állapotban (2) adja a kapcsolatban
ahol tetszőleges pontja oldalfelületének a henger.
Feltételek (6) lehet azonosan zajlik csak akkor, ha a száma a henger részben kerülete.
Állapot (3) az eltűnő a kapott vektor erők
végrehajtani, ha a tengely átmegy a súlypont a szakasz.
Állapot (4) a pillanatok végén a henger formájában
Így kerek rúd teljes mértékben lehetséges, hogy össze egy megoldást, mivel a szög csavar határozza meg az első feltétel (7):
ahol a másodrendű nyomatékot tengelyhez képest
Az általános esetben, ha a keresztmetszet nem kerek gépe torziós torzult, ezért keresik a megoldást az elmozdulás formájában
Akkor nem nulla feszültség és a stressz:
egyensúlyi körülmények között (1) vezetnek az egyenlet a funkciót
Ekkor (2) hiányzik az erőfeszítés oldalán az egyenlet az egyenértékű részén a kontúrpontok
Tekintettel arra, hogy egy tetszőleges pont a kontúr
átírni a feltétel (11) formájában
Így tekintve a (10), amely egy torziós funkció csökkenti a megoldása Neumann problémát. Ahhoz, hogy működjön, a konjugátum a harmonikus függvény
. azaz a feltételeket Cauchy-Riemann kapott (12)
Ez azt jelenti, fordult a Dirichlet probléma. Az állandó integráció vesz érték esetén halmozottan szakasz kontúrjait az egyes körök.
Ha bevezetjük a stressz funkció, megkapjuk
A stressz funkciója megfelel a Poisson-egyenlet
A peremfeltétel
minden szakasz kontúrok, ha szaporodnak.
Mi ellenőrizze a nulla a kapott vektort a ható erők a végén a rúd. mert
Találunk végén a nyomaték rúd
ahol a határolt területen ötödik többszörösen áramköri rész a határoló, ahol a külső hurok, és a többi áramkör állandókat határoztuk meg a folytonosság feltétele elmozdulásvektorból a bypass hurok.
Kiszámításakor az integrált belső kontúrok a határ tekinthető, hogy a bypass elhagyja a területet a bal oldalon, valamint az a tény, hogy
ha ez a terület a régió által határolt kontúrt.
Az egyszerűen csatlakoztatott áramkört
A multi-loop
A tétel a keringési nyírófeszültség. Meghatározása állandó több területen áramköri rész.
A tétel a tangens cirkuláció bármilyen zárt áramkör feszültsége:
I =. ahol a terület által határolt
A számítás figyelembe veszi a forgalomban a (8) képletű mozogni
és (9) általános feszültségekhez
Behelyettesítve a kifejezés a stressz forgalomba szerezni
Mivel a egyediségét elmozdulást, amikor áthalad a kontúr integrál
Alkalmazva a tételt a forgalomból az egyes belső kontúrja határának többszörösen, kapunk egy egyenletrendszer meghatározásához
Mi ellenőrizze a példában kapott eredményekkel kontúr által határolt két koncentrikus kör a külső sugár és a belső sugara.
Feltételek nullával egyenlő a külső felületen lehet végezni, ha a feszültségek keresni funkciót formájában
A helyettesítés után a Poisson-egyenlet, megkapjuk
Alkalmazzuk a tétel a vérkeringést a belső kontúr
Így ez a stressz funkciója megfelel a feltételeknek a probléma.
Találunk működő ponton közvetlen kiszámítása és a képlet (17):
Torziós a henger ellipszis keresztmetszetű
Tekintsünk egy henger, a keresztmetszet körvonala, amely egy ellipszis.
Mi kell keresni a stressz funkció formájában
ami egyértelműen az áramkörben nulla. Ez a Laplace operátor
ahonnan találunk sonstantu
A maximális nyírófeszültség eléri a felületet, és egyenlő
Idő kiszámítására fogja találni a kapcsolatot a torziós szög
Torziós négyszögletes keresztmetszetű.
Tekintsük a torziós rúd a négyszögletes keresztmetszetű:
Mi kell keresni a stressz funkció formájában egy sor
Amikor egy ilyen bővülés a határokat Behelyettesítve (20) a Poisson-egyenlet
Szorozzuk meg a bal és jobb oldali, és integrálni át megelőzően, mivel az ortogonális függvény, azaz a
Számvitel (22), miután az integráció vezet a következő egyenleteket a funkciók:
Egyesített oldatot az említett feltételeket kielégítő
Így a stressz funkció megtalálható formájában sorozat:
Megtaláljuk a megoldást más módon. Tekintsünk egy négyszöget, amelyben. Ezután értelmében a peremfeltételek, ha lehet keresni egy megoldás formájában
A (24), a függvény kielégíti a harmonikus egyenletet. Ha, mint a múltban, hogy megoldja a problémát az elválasztási eljárás változók, függvények, hogy homogén egyenlet
Mert kell még megoldást, megkapjuk
Találunk az állandó a feltételt. Ehhez megszorozzuk
, és integrálni át megelőzően.
Az eredmény:
Ellentétben megoldások (25) (23) -ból azért fontos, mert a számát összeadjuk, és a fennmaradó sorozat konvergál gyorsan.
Ha úgy találja, az idő és a maximális nyírófeszültség, megkapjuk:
Mert profilok formájában vékony csíkokra szélességű és hosszúságú
és nyitott profilok, amely több szalagok
Torziós vékonyfalú bár egy többszörösen listájában.
Tegyük fel, hogy a rúdnak egy vékony falú többszörösen régió (2. ábra). Feltételezzük, hogy a vastagsága sokkal kisebb, mint a görbületi sugár
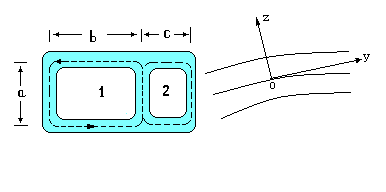
Ábra. 2 vékony falú rúd részén többszörösen
Ezután a kiválasztott falak falelem lehet tekinteni párhuzamosan, és az oldatot gyengén függő változó. Ebben az esetben, a Poisson-egyenlet felírható körülbelül a
Egyenlet megoldása (26) peremfeltételek ad stresszfüggvény
E közelítés Mivel az érték kicsi, a második tag lehet elhanyagolni, és állandónak tekinthető nyírófeszültség
Alkalmazzuk a tétel a forgalomban a nyírófeszültség az egyes áramkör (2. ábra két ilyen áramkörök). Így a külső áramkörtől feltételezzük állandó, mint nulla, a kontúr 1, azt feltételezzük, hogy legyen egyenlő, és a kontúr 2, egyenlő
Megoldása a kapott rendszer állandó, azt látjuk,
Ha feltételezzük, az azonos vastagságú, egyszerűsített képlet