A labda súly 0, 15 kg megüti a sima fal szögben 30 fok hozzá

Állapota a problémát:

A labda súlya 0,15 kg megüti a sima fal szögben 30 ° hozzá, és pattan veszteség nélkül a sebesség. Találja meg az átlagos kifejtett erő a labdát a falak, amikor a labda sebessége 10 m / s, és a hatása időtartama 0,1 s.

№2.1.37 feladata a „Collection feladatok előkészítése a felvételi vizsgák a fizika UGNTU”

\ (M = 0,15 \) kg, \ (\ alpha = 30 ^ \ circ \), \ (\ Upsilon = 10 \) m / s, \ (\ Delta t = 0,1 \) c \ ( F -? \)

Megoldás:

Ható erő a labdát az egyik oldalfal, megtalálható Newton második törvénye írt általános formája:

Ebben a képletben, \ (\ Delta p \) - a változás impulzus labdát, hogy ütött a falnak, \ (\ Delta t \) - ismert körülmények között a kölcsönhatás.

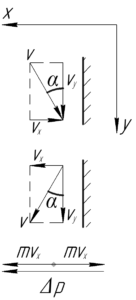
Keressük a változás lendület a labdát. Az ábrán a pillanatokban közvetlenül megelőzően és követően azonnal fúvócsúcs. Mivel a sebesség és nem áldozatot, a hatás tekinthető teljesen rugalmas, így a labda lepattan ugyanolyan szögben. Kivetítése labda sebességét előtt és után a hatás \ tengely (x \) és \ (y \).

Látható, hogy a tengely mentén \ (y \) (\ upsilon_y \) sebessége vetítési \ egyenlő előtt és után hatása \ (\ Upsilon \ cos \ alpha \), ezért, megváltoztatja a labdát impulzus ebben az irányban nem volt, és azt jelenti, ebben a tekintetben és nem erő.

Tengelyirányban \ (x \) modul mozgásmennyiség-változás mértéke (lásd az alsó része a rendszer):

\ [\ Delta p = 2m = 2m \ Upsilon \ sin \ alpha \; \; \, \, (2) \]

Behelyettesítve (2) be (1) megkapjuk a megoldás a probléma általánosságban.

Helyettesíti az adatokat a probléma ebben a képletben, úgy véljük, a számszerű választ.

Válasz: 15 N.

Ha tetszik a probléma és annak megoldása, akkor ossza meg ismerőseivel Ezekkel a gombokkal.