A dot termék két vektor - studopediya
A geometriai vektor belső szorzata határozza meg azok geometriai jellemzői és meghatározása a következő:
Ez a kifejezés átírható szempontjából koordinátáit (itt a képlet a háromdimenziós térben):
4.) kollinearitás és coplanarity
Vektor párhuzamosan ugyanazon egyenes vonal vagy egy sorban nevezzük kollineáris vektorok
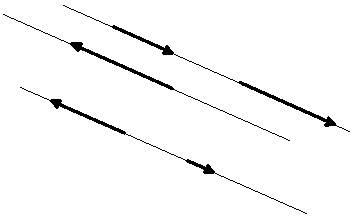
Feltételek kollineárisak vektorok
Két vektor egy egyenesbe esik, ha a fenti feltételek bármelyike:
1. Két a és b vektorok egy egyenesbe esik, ha létezik olyan n szám olyan, hogy
2. Két vektorok kollineárisak Ha az arány a koordinátáival egyenlő.
Nota bene 2. feltétel nem alkalmazható, amikor az egyik komponens a vektor nulla.
3. Két vektor egyenesen vannak, ha a vektor termék megegyezik a nulla vektor. A kereszt terméket Két vektor a = b = és a derékszögű koordináta-rendszerben, - egy vektor, amely érték kiszámítható a következő képlettel: A x B = mátrix i j k ax ay AZ bx a bz, vagy egy X b = = Sparal
Nota bene 3. feltétel csak akkor kell alkalmazni háromdimenziós (térbeli) problémákat.
Három vektor (vagy több) nevezzük egy síkban, ha ők is adni a közös eredet, hazugság ugyanabban a síkban.
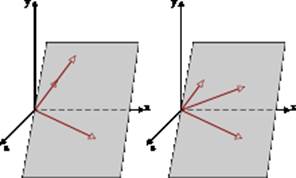
Let - vektorok a teret. Ekkor a következő állítások igazak:
1. Ha legalább az egyik a három vektor - nulla, akkor a három vektor is tekinthető egy síkban vannak.
2.Troyka tartalmazó vektorokat egy pár kollineáris vektorok, egy síkban vannak.
3.Smeshannoe termék síkban vektorok. Ez - a kritériumát coplanarity három vektorok.
Coplanar vektorok - lineárisan függ. Ez - szintén kritérium coplanarity.
4.Suschestvuyut valós számok, hogy egy síkban vannak. kivéve azokat az eseteket, vagy. Ez - mely újra a korábbi ingatlan, valamint a kritérium coplanarity.
5. A 3-dimenziós tér három nem egy síkba eső vektor képezi alapját. Vagyis bármely vektor lehet kifejezni :. Aztán fogja koordinálni az adott alapot.