Parabola, analitikus geometria
A parabola a pályája pont, amelyek mindegyike a távolság egy fix pont a síkban, az úgynevezett fókuszpont, egyenlő távolság egy rögzített egyenes vonal, az úgynevezett direktrixét. A hangsúly a parabola által kijelölt F betűvel, a távolság a fókuszt direktrixét - a levél p. A szám p nevezzük paraméter a parabola.
Legyen adott egy parabola. Egy derékszögű derékszögű koordináta-rendszert úgy, hogy az x-tengely áthalad
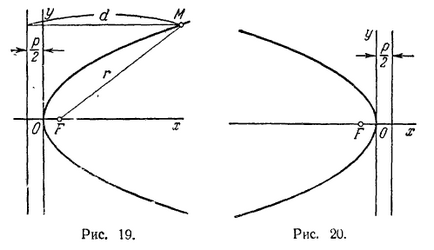
Ez parabola fókuszpontjának és merőleges a direktrix a direktrix került a tekintett fókuszpontba irányított; A származási félúton található a fókusz és az direktrix (ábra. 19). Ebben a koordinátarendszerben, ez parabola határozza meg az egyenlet
(1) egyenlet az úgynevezett kanonikus egyenlete parabola. Ugyanebben koordinátarendszer direktrixét a parabola egyenlete
Focal sugara egy tetszőleges pont M (x, y) a parabola (.. Ie FM szegmens hossza) lehet kiszámítani a következő képlettel
A parabola van egy szimmetriatengelye, az úgynevezett tengelye a parabola, amely metszi egy ponton. A metszéspontja a parabola tengelyével nevű csúcsa. Ha a fenti koordinátarendszerben adja meg a parabola tengelye egybeesik a vízszintes tengelyen a csúcs a származás, az egész parabola fekszik a jobb oldalán.
Ha a koordináta-rendszer úgy van megválasztva, hogy az x tengely tengelyével párhuzamossá a parabola, az eredete - egy vertex, de a parabola rejlik a bal felét (. Ábra 20), akkor az egyenlet lesz formájában
Abban az esetben, ha a származási és a felső egy vonalban van a tengelye az ordináta, a parabola lesz az egyenlet
ha ez fekszik a felső felét (ábra. 21), és a
- ha az alsó felét (ábra. 22)
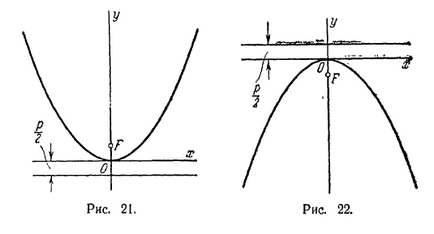
Mind a parabola egyenlet (2), (3) és (4) a (1) egyenlet az úgynevezett kanonikus.
583. Keresse meg az egyenletet a parabola, a csúcsa, amely a származási, tudván, hogy:
1) a parabola szimmetrikusan elrendezett a jobb felét a tengelyhez képest Ox és p paraméter = 3;
2) a parabola szimmetrikusan elrendezett bal felét a tengelyhez képest Ox és annak P-értéke = 0,5;
3) a parabola szimmetrikusan elrendezett felső felében képest az y-tengelyen, és annak a paraméter p = 1/4
4) a parabola szimmetrikusan elrendezett alsó felében képest az y-tengelyen, és annak p paraméter = 3.
584. Annak megállapításához, a helyét és méretét a paraméter tekintetében a koordináta tengelyeket a parabola következő:
1) Y 2 = 6x; 2) x 2 = 5u; 3) y = 2 - 4; 4) x 2 = - y.
585. Keresse meg az egyenletet a parabola, a csúcsa, amely a származási, tudván, hogy:
1) egy parabola szimmetrikus tengelyéhez képest Ox és áthaladjon a pont (9, 6);
2) egy parabola szimmetrikus tengelyéhez képest Ox és áthaladjon a B pont (1, 3);
3) egy parabola szimmetrikusan elrendezett tengelyhez képest O, és áthalad azon a ponton, C (1, 1).
4) egy parabola elrendezve szimmetrikusan az y tengely és az áthalad a D pont (4-8).
586. Az acél kábel felett felfüggesztett két végét; rögzítési pontok találhatók ugyanabban a magasságban; a köztük levő távolság egyenlő a 20 m. A elhajlását a parttól 2 m-re a rögzítési pont, feltételezve, hogy a vízszintes 14,4 cm. Határozzuk meg értékét kábelváiyú közepén kapcsolódási pontok között, mintegy feltételezve, hogy a kábel formájában íven egy parabola.
Létrehozása 587. Az egyenlet a parabola, amelynek a fókusz E (0, -3), és áthalad a származási, tudva, hogy a tengelye az y tengelyen.
588. Annak meghatározásához, amelyek vonalak határozzák meg a következő egyenletek:
1) y = + 2√h; 2) y = + √ (- x); 3) y = - 3 √ (- 2);
4) y = - 2 √x; 5) x = + √ (5Y) 6) X = - 5√ (- y);
7) X = - √ (3y); 8) X = + 4√ (- y);
Ábrázolják ezeket a sorokat a rajzban.
589. Keresse meg az egyenletet a fókusz F és direktrix a parabola y 2 = 24x.
590. Compute a fókuszpontja a sugara M a parabola y 2 = 20x, ha az abszcissza az M pont egyenlő 7.
591. Compute a fókuszpontja a sugara M a parabola y 2 = 12x ha az ordináta az M pont egyenlő 6.
592. A parabola y 2 = 16x lelet pont fokális sugara 13.
Létrehozása 593. Az egyenlet a parabola, a hangsúly adnak, ha az F (-7; 0), és az egyenlet direktrix X - 0 = 7.
594. létrehozása parabola egyenlet, tudva, hogy a csúcsa egybeesik azzal a ponttal (α, β), a p paraméter, a tengellyel párhuzamos Ox és egy parabola a végtelenbe terjed:
1) a pozitív iránya az X tengely mentén;
2) a negatív irányban az X tengely.
595. létrehozása parabola egyenlet, tudva, hogy a csúcsa egybeesik azzal a ponttal (α, β), a p paraméter, párhuzamos tengely az y tengely és a parabola a végtelenbe terjed:
.. 1) a pozitív iránya az y-tengely (azaz, a parabola az uplink);
2) a negatív irányba az y-tengely (R. F. Pas Rabolu van csökkenő).
596. Annak megállapítására, hogy az egyes a következő egyenlet határozza meg a parabola, és hogy megtalálják a koordinátáit a csúcsok A paraméter értékét p és direktrixét egyenlet: 1) y 2 = 4-8; 2) y 2 = 4 - 6x; 3) 2 = x 2 + 6Y; 4) x 2 - 2 - y.
597. Annak megállapítására, hogy az egyes a következő egyenlet határozza meg a parabola, és hogy megtalálják a koordinátái a csúcsokat és a paraméter értékét p: 1) y = 1,4 x + 2 x + 2; 2) y 2 = 4x - 8x + 7; 3) y = -1 / 2 + 6 x 2-7.
598. Annak megállapítására, hogy az egyes a következő egyenlet határozza meg a parabola, és hogy megtalálják a koordinátái a csúcsból, és a paraméter értékét p: 1) 2 x = 2y - 12y + 14;
2) X = - 1 / 4Y 2 + y; 3) x = y 2 + 2y - 1.
599. Annak meghatározására, hogy mely vonalak által meghatározott, a következő egyenletek-képző:
1) y = 3-4 √ (X - 1); 2) X = -4 + 3√ (y + 5);
3) X = 2 - √ (6 - 2y); 4) y = - 5 + √ (-ZH - 21).
Ábrázolják ezeket a sorokat a rajzban.
600. létrehozása parabola egyenletet, ha az adott a hangsúly F (7, 2), és direktrix X - 5 = 0
601. létrehozása parabola egyenletet, ha az adott a hangsúly F (4, 3) és a direktrix y + 1 = 0.
602. létrehozása parabola egyenletet, ha az adott a hangsúly F (2; 1), és direktrix x - y - 1 = 0.
603. Tekintettel a parabola csúcsa (6; 3) és annak direktrix egyenlet 3x - 5Y + 1 = 0, Find a hangsúly F a parabola.
604. Tekintettel a parabola csúcsa (-2; - 1) és annak direktrix egyenlete x + 2y - 1 = 0. létrehozása egyenletet a parabola.
605. Határozza meg a metszéspont a vonal x + y - 3 = 0, és parabola x 2 = 4Y.
606. Határozza meg a metszéspont a vonal Sx + 4y - 12 = 0, és a parabola y = 2 - 9h.
607. Határozza meg a metszéspont a sor Sx - 2y + 6 = 0, és a parabola y = 2 6x.
608. A következő esetekben, meghatározza, hogy ez a viszonylag egyenes ez a parabola - metszi-e ér vagy túlnyúlik ez: 1) x - y + 2 = 0, y 2 = 8x; 2) 8x + 3y - 15 = 0, x = 2 -3u; 3) 5 × y - 15 = 0, Y = 2 - 5x.
609. Határozza meg, amelyre értékekkel: k a lejtőn y = kx + 2 1) metszi a parabola y = 2-4; 2) Ami azt; 3) nyúlik ki a parabola.
610. Vezessük a feltételt, amelynek az egyenes y = kx + b tekintetben parabola y 2 = 2px.
611. Annak bizonyítására, hogy a parabola az y 2 = 2px fér egy és csak egy érintőleges a szögletes k együtthatót ≠ 0.
612. létrehozása egyenlete az érintő a parabola y 2 = 2px annak ponton M1 (x1; y1).
613. létrehozása lineáris egyenlet, amely kapcsolódik a parabola y = 8x 2, és párhuzamos vonal 2x + 2y - 3 = 0.
614. létrehozása lineáris egyenlet, amely kapcsolódik parabola x 2 = 16U, és merőleges a vonal 2x + 4y + 7 = 0.
615. végre egy érintőleges a parabola y 2 = 12x párhuzamos vonal Sx - 2y + 30 = 0, és kiszámítja a távolságot d közötti az érintő és az adott sorban.
616. A parabola y 2 = 64x megtalálni azt a pontot az M1. legközelebb a vonal 4 + Zy - 14 = 0, és kiszámítja a távolságot d a pont M1 az egyenes vonal.
617. Írja az egyenletek az érintők, hogy a parabola az y = 2 ZBH húzott pont (2, 9).
618. A parabola y 2 = 2px érintők. Igazoljuk, hogy a csúcsa a parabola közepén fekszik közötti metszéspontja az érintő és az x-tengely, és a nyúlvány a tapintási pont az x tengelyen.
619. A pontból (5; 9) tartott érintő a parabola y 2 = 10x. Írja az egyenletet az összekötő húr az érintési pontot.
620. tól P pont (-3; 12) tartott érintő a parabola y 2 = 10x. Számítsuk ki a d távolság a P pont, hogy a húrt a parabola, amely összeköti az érintkezési pontnál.
621. Határozza meg a metszéspontja az ellipszis x 2/100 + y 2/225 = 1, és a parabola y 2 = 24x. x *
622. metszéspontját meghatározó a hiperbola x 2/20 pont - y 2/5 = -1, és a parabola y = Sx 2
623. Annak megállapításához pontok metszi a két parabola: y = x 2 - 2x + 1, x == y 2 - 6Y + 7.
624. Annak bizonyítására, hogy a vonatkozó sorban a parabola egy bizonyos ponton M jelentése azonos szöget zárnak be a sugara a fókuszpont M és egy gerenda, hogy az M, párhuzamosan fut a tengelye a parabola az irányba, ahol a parabola kiterjeszti a végtelenségig.
625. A hangsúly a parabola y 2 = 12x hegyesszögben α, hogy az x-tengelyre irányul a fénysugár. Köztudott, hogy a tga = 3/4. Amikor elérte a parabola, a fénysugár visszaverődik. Legyen közvetlen egyenlet, amely a visszavert fény.
626. Annak bizonyítására, hogy a két parabola, amelynek egy közös tengely és egy közös téma között található a csúcsok metszik derékszögben.
627. Bizonyítsuk be, hogy ha a két parabola kölcsönösen merőleges tengely metszéspontját négy ponton, ezeket a pontokat feküdni egy kört.