Egy egyenlő szárú trapéz beírt kör
Ha az egyenlő szárú trapéz beírt kör, számos módja van, amelyek segítségével vezeti a megoldást a problémára.
1. egy egyenlő szárú trapéz beírt kör, amely érinti egy pont osztja az oldalsó hosszúságúra m és n. Keresse meg a terület trapéz.
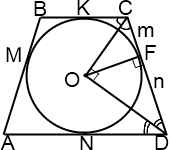
2) Mivel a központ a beírt kör - metszéspontjában szögfelezői trapéz, a
3) Mivel az összeget a háromszög szögeinek 180 °. a háromszög OCD ∠ COD = 90 °.
4) A merőleges CD (mint a sugár hívni az érintkezési pont), úgy, hogy a háromszög OCD - magassága hívni átfogója. By ingatlan derékszögű háromszög.
Mivel a magassága a trapéz egyenlő az átmérője a beírható kör,
5) A képlet megtalálásához a területet a trapéz
Mivel a trapéz a beírt kör, az összege a szemközti oldal egyenlő:
Így a terület a trapéz egyenlő
2. egyenlő szárú trapéz beírt kör, amely érinti egy pont osztja az oldalsó szegmensekre és m n.Nayti kerülete trapéz.
AB = CD (a hipotézis).
AD + BC = AB + CD (mivel trapéz beírt kör).
3. Az egyenlő szárú trapéz beírt kör. Keresse meg a magassága a trapéz, ha tudjuk, hogy az alapítás: AD = a, BC = b.
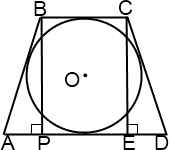
Döntött háromszögek háromszögek ABP és a DCE vannak a lábát, és a átfogója. Ennélfogva
Mivel a trapéz beírt kör, AB + CD = AD + BC = a + b,
A háromszög ABPpo Pitagorasz-tétel
Ha az egyenlő szárú trapéz beírt kör, a magassága a trapéz átlagos arányos között annak alapjait.