archimédeszi test
A geometriában archimedesi test (Archimedes polihedron) - nagymértékben szimmetrikus semiregular konvex poliéder. oldalait, amelynek két vagy több típusú szabályos sokszög. szomszédos azonos magasságban. Ezek eltérnek a platóni testek (szabályos testek) is, amelyekre csak egyféle sokszög csúcsai azonos, és a Johnson poliéder. szabályos sokszög arcok, amely tartozik a különböző csomópontok.
Itt, a „azonos csúcsokat” azt jelenti, hogy bármely két csúcsa van izometria az egész test, átalakítja egyik csúcsa a másik. Néha csak arra van szükség, hogy a pereme a felső izometrikus arcok voltak a tetejére a másik. Ez a különbség a definíciók meghatározására, hogy figyelembe vegyen egy hosszúkás négyzet girokupol (pszeudo-Rombo-cubo-oktaéder) archimedesi szilárd vagy poliéder Johnson - az egyetlen konvex poliéder, amelyben a sokszög felületek szomszédságában, hogy a tetején egy és azonos módon minden egyes tetején, de a poliéder nem ez egy globális szimmetria, ami lefordítja bármely csúcspont bármely más. Alapján a létezését ál-rombusz-cubo-oktaéder, Grunbaum [1] javasolt egy terminológiai különbség, ahol a archimedesi testet úgy definiáljuk, mint az azonos csúcsa alak minden egyes csomópont (beleértve a hosszúkás négyzet girokupol), míg homogén poliéder [en ] határozzuk meg, hogy bármilyen top, bármely más szimmetrikus (amely kizárja girobikupol.
Antiprisms prizma. csoportok, amelyek az diéderes szimmetria-csoport. általában nem tekinthető archimédeszi testek, annak ellenére, hogy azok nem esnek a fenti definíció. Ezzel a korlátozás, csak véges számú felhajtóerő szervek. Minden a testre, kivéve a hosszúkás négyzet girokupola kaphat wythoff építőiparban a platóni testek felhasználásával tetraéderes. oktaéderes [en] és ikozahedrális [en] szimmetria.
Archimedesi szilárd nevű Archimedes. beszéljük meg a most vesztették el állásukat. Papp utal, hogy ez, és azt kéri, hogy Archimedes felsorolt poliéderek 13 [1]. A nap a reneszánsz művészek és matematikusok értékes tiszta formák és felfedezte mindet. Ezek a vizsgálatok arra majdnem teljesen befejeződik körül 1620 Johannes Kepler. [2] amely meghatározott fogalmát prizmák. antiprisms és a nem-konvex testek, úgynevezett Kepler teste - Poinsot.
Vannak 13 archimedesi szilárd (nem beleértve a hosszúkás négyzet girokupola, 15, adott egy tükör a két enantiomer külön vannak felsorolva az alábbiakban.).
Itt a vertex konfiguráció utal, hogy a típusú szabályos sokszögek, amelyek szomszédosak a felső. Például, apikális konfiguráció (4,6,8) azt jelenti, hogy egy négyzet. hatszög és nyolcszög találkozik csúcsánál (a sorrendben a vett óramutató járásával megegyező irányban képest a vertex).
név
(Alternatív cím)
A csúcsok száma 720 ° -kal a szögletes hiba a tetején.
Cuboctahedron és ikozidodekaéder vannak szélű homogén [en] és a hívott quasiregular.
királis
Simous simous kocka, és a dodekaéder aszimmetrikus. ahogy azok megjelennek a bal oldali és a jobb oldali változat. Ha valami van néhány faj, amely háromdimenziós tükörképe egymásnak, ezeket a formákat nevezzük enantimorfami (ez a név is alkalmazzák valamilyen formában a kémiai vegyületek).
Az építőiparban a felhajtóerő szervek
További információk: Egységes poliéderek és poliéderek jelölést Conway
Archimedesi szilárd anyagok felhasználásával épült a generátor helyzetben egy kaleidoszkóp
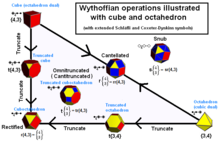
A test különböző plátói és archimedesi nyerhető egymástól néhány műveletek. Kezdve a platóni testek, akkor csonkolás szögek. Megőrizni a szimmetria a csonkolás merőleges síkban összekötő vonal a sarokban a központtól a sokszög. Attól függően, hogy milyen mély a csonkolás végeztük el (lásd. Az alábbi táblázatot), megkapjuk a különböző plátói és archimédeszi (és mások) a szervezetben. Nyújtás vagy kaszálás végzi mozgását arcok (irány) a központtól (az azonos távolságra, hogy fenntartsák szimmetria), és a létrehozása, majd a konvex burok. Bővülő forgatni is forgatásával szempontjára, megtöri téglalapok előforduló területén élek háromszögekre. A közelmúltban, az építési amelyet mi adunk itt meg van rövidítve mind a sarkok és élek. Ha figyelmen kívül hagyja a skála a terjeszkedés lehet tekinteni, mint csonkolt sarkok és élek, de egy bizonyos kapcsolat a csonkítások a szögek és élek.
Az építőiparban a felhajtóerő szervek
tetraéderes