9 előadás Matlab (optimalizálás, lineáris programozás)
Matlab. Optimization, lineáris programozás.
Keresés extrém egyváltozós függvényeket. Helyi keresés (egy bizonyos tartományon belül) a minimális ellátja a funkcióját [x, y] = fminbnd (FunctionName, granitsyIntervala). Ha szükség van, hogy megtalálja a helyi minimum a funkció, amely az előzőtől eltérő megjelölés és keresi legalább, ami valójában a maximumot. Ha ez a funkció az érték a legnagyobb mért érték a másik védjeggyel.
Keresés szélsőséges függvényében számos változó. Ha a funkció kerül kiszámításra számos változótól, majd megtalálja a minimális alkalmazunk (miután a kezdeti közelítő becslés közelítő változók a feltételezett minimális) parancs [x, y] = fminsearch (FunctionName, vektorNachalnyhPriblizheniyPeremennyh).
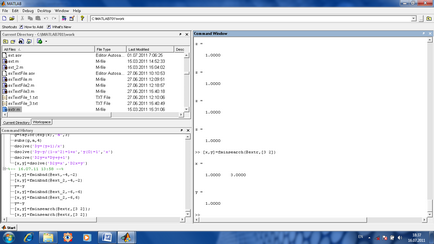
A megoldás a lineáris programozási feladatok. A problémák a lineáris programozás szükséges, hogy megtalálják a maximum vagy minimum egy lineáris függvény többváltozós lineáris megszorítások formájában egyenlőségek és egyenlőtlenségek. Vegyük például a következő probléma.
Legyen a függvény L (x1, x2, x3, x4) = x1 + x2 + x3 + x4, és meg kell találni a legnagyobb és a vonatkozó maximális értékeket a változók.
Tegyük fel, hogy az egyenlőtlenség korlátok. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0.
Tegyük fel azt is, hogy továbbra is korlátozások formájában egyenlőtlenségeket.
Hogy oldja meg a lineáris programozási feladat (megtalálása a minimális) használjuk a funkciót [x, L, f] = linprog (c, a, b, A1, B1, Lx, Rx), ahol
x vektor értékeit a változók kapott, mint a válasz; L értékét a függvény a legkisebb;
f paraméter jellemző számítási folyamat (ha nulla, akkor az oldatot felfüggesztették, miután elérte a maximális iterációk száma, ha pozitív, akkor minden rendben határozott, ha a döntés negatív nem található);
c célfüggvény képviseli, mint egy vektor együtthatók (ebben az esetben [1 1 1 -1], de mivel szükségünk van a maximális, és a funkciót [x, L, f] = linprog (c, a, b, A1, B1, Lx, Rx) keresések legalább szempontjából a függvény megváltoztatja jel, így az együttható vektor [-1 -1 -1 1]);
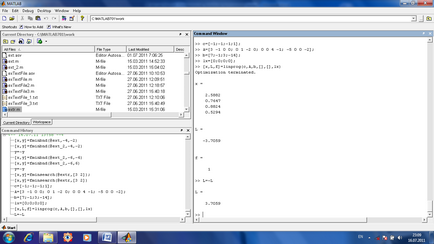
A, b rendszer korlátai meghatározott mátrix formában Ax≤b (a mi probléma korlátozás 3x1 -X2 ≤7, x2 -2x3 ≤-1, 4x3 -X4 ≤3, 5x1 + 2x4 ≥14, de mivel 5x1 + 2x4 ≥14 nem alkalmas, szükséges megváltoztatni a jele egyenlőtlenség ebben az esetben ez lesz -5x1 -2x4 ≤-14, ebben az esetben a mátrix a áll együtthatók (a változók) ezeket az egyenlőtlenségeket, és az oszlop b áll jobb (nem tartalmazó változók ) oldalán a egyenlőtlenségek;
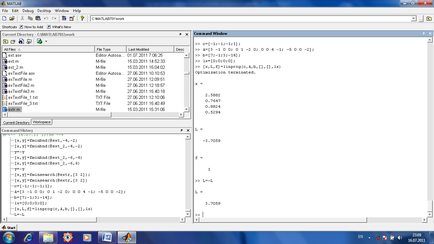
A1, B1 rendszere egyenletek formájában A1x = b (a mi probléma az ilyen rendszer nincs korlátozás, de lehet);
Lx, Rx kapcsolódnak korlátozások formájában Lx≤x≤Rx, Lx≤x, x≤Rx (a mi a probléma van korlátozott típusú Lx≤x, így Lx vektor 0 0 0 0).
Amikor linprog funkció használható a paraméterek listája helyett azok, amelyek nem szerepelnek, tedd az üres szögletes zárójelek.
Nézzünk egy példát egy edzést. Adott egy függvény W = x1 + x2 + 3x3 -X4 és meg kell találni a maximumot. Tegyük fel, hogy az egyenlőtlenség korlátok.
Mi a probléma megoldására a funkciója [x, L, f] = linprog (c, a, b, A1, B1, Lx, Rx). Annak alkalmazására, van, hogy felkészítse az érveket, hogy a funkciót. A vektort az együtthatóknak a függvény egyenlő (1, 1 3 -1), de függvényében legalább linprog keres, és szükségünk van egy maximális, majd módosítsa a jele az együtthatók a funkció és azután a vektort (-1 -1 -3 1). A mátrix áll az együtthatók a változók a rendszerben az egyenlőtlenségek x1 -5x2 + 4x3 ≤5, x1 -2x2 -3x3 ≤4, x1 + 6x2 + 5x3 ≤4, x2 + x3 ≤1. Mivel ezek mind ismerik ≤ nem szükséges változtatni semmit. A b vektor áll a jobb oldalán azonos egyenlőtlenségeket. A1 mátrix A1h = b1 rendszer nem releváns számunkra (nincsenek ilyen körülmények között). Lx, Rx kapcsolódnak korlátozások formájában Lx≤x≤Rx, Lx≤x, x≤Rx. Van egyenlőtlenség korlátokat. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0. Ezután a vektort Lx = [0; 0; 0; 0]. Mint más típusú korlátozásokat, akkor, mivel nincs ilyen korlátozás, hogy nem fontos a számunkra.
nem-lineáris programozási feladat. A nemlineáris probléma különbözik a lineáris. Ez egy olyan rendszer lineáris egyenlőtlenségek Ax≤b, a lineáris egyenletrendszer A1x = b1, rendszer lx≤x≤rx típusú korlátozásokat, lx≤x, x≤rx. Eltekintve azonban ezeket az ismerős (a lineáris programozás) feltételek, van egy olyan rendszer, a nemlineáris típusú g1 (x) ≤0 korlátok, és a nemlineáris egyenletek g2 (x) = 0. Hogy oldja meg a nemlineáris programozási feladat (szelekció után vektor x0 kezdeti közelítés) használjuk a funkciót [x, y, f] = fmincon (F, x0, A, B, A1, B1, Lx, Rx, G), ahol G jelentése egy M-funkció amely kiszámítja a bal oldali részén a nemlineáris korlátok g1 (x) ≤0, g2 (x) = 0. Ha bármely érvek nincsenek megadva, akkor cserélje ki a függvényhívás kerülnek szögletes zárójelben.
Vegyük például a következő probléma. Legyen egy függvény x1 2 + x2 2 = 1, azzal a megkötéssel, hogy X1, X2 = 4, x1 ≥0, x2 ≥0. Vektor kezdeti közelítések vegye egyenlő x0 = (0,1, 0,1).