Mi a sorsa, vagy hogyan ne veszítse - Sportprognoz

Tanár védett titkot!
Mi Fortune, a boldogság minden törzs
Holding a karmai a győzelem?
Dante. Az Isteni színjáték.
Pokol. VII, 67-69
Iskola folklór tartalmaz egy történetet egy ember, aki kifejlesztett egy számítógépes rendszert a játék, „Sport Lottó”, és elnyerte a szerencse. Ez az ember még nem látott, és nem valószínű, hogy létezik olyan bizonyosan nyerő stratégia ebben a játékban nem. Más szóval, akkor nem határozható meg olyan módon, hogy a játék, amelyben a nyert összeget mindig nagyobb, mint a pénz beszerzésére fordított kártyákat. Ők sem kivételek és stratégiák általunk kínált. Azonban a „Sport Lottó” és más hasonló játékok kötve, sok érdekes matematikai problémákat. Néhány közülük fogjuk mondani.
7 * 10 -8; ugyanolyan jelölésekkel p (49,5)
3 x 10 -6 (tudod bizonyítani magának).
A „Sportprognoz” játszott az alábbiak szerint. Naptár sportesemények 13 kiválasztott játékok, amelynek kimenetele szerint a szervezők a sorsolás, nehéz megjósolni. A játékosnak, hogy az előrejelzés az eredményeit a mérkőzést, forgalomba mind a 13 sejtek az asztal a jel „1”, ha azt hiszi, hogy a hazai csapat nyeri, a „2” - a vendégcsapat, és a „0” esetén a döntetlen. Miután a pontszámok ismertek, határozza meg a győztes kártyákat. Díjat megosztva Guess nem kevesebb, mint 11 eredmények, és növeli a számos helyes előrejelzéseket a kártyát. Minden becslés lesz a 13-dimenziós vektort (azaz, egy sor 13 szám) a komponensek 0, 1 és 2 Például, a vektor x = (1,1,0,2,2,1,2,0,0, 0,1,1,2) megfelel a nyereség felülvizsgálatok 4, 5, 7 és 13 mérkőzések a hosts - 1, 2, 6, 11 és 12, és megegyezik az egyik a - más üléseken.
A „Sport lottó” játék megköveteli kitalálni, vagy 6 49 5 36 számot. A győztes az a kártya, amely jelezte, legalább 3 az elválasztott eredményeként a sorsolás a számok. Predikció alkalmazása ebben az esetben lehet leírt 49- (36-) dimenziós vektor, amely egy „0” 43 (31) helyzetben, és „1” 6 (5) fennmaradó pozíciókban. Nem egyes pozíciók megfelelnek az előre jelzett számokat.
Az egyes, az egyiknél játékos hez több változatban az előrejelzés. Felhívjuk a készlet ezeket a lehetőségeket, l-rendszert, ha eredményétől függetlenül a keringési köztük van legalább egy olyan, amelyben helyesen találgatás legalább l eredményeket. Mi érdekli csak l-11 rendszer<=l<=13 для «Спортпрогноза» и с 3<=l<=6 (5) для «Спортлото». Очевидные примеры l-систем с максимальным l получаются при заполнении всех возможных вариантов прогноза. Эти системы не очень интересны хотя бы потому, что количество заполняемых при этом карточек «Спортпрогноза» равно 1 594 323, т.е. нужно затратить около полумиллиона рублей и около двух лет непрерывной (по полминуты на карточку) работы. Для «Спортлото» соответствующие числа ещё больше. Плохо и то, что, даже справившись с заполнением, нельзя быть уверенным в том, что сумма выигрыша превзойдет сделанные затраты. Для меньших l мы будем стараться придумать такие системы, в которых общее число вариантов было бы как можно меньше.
Tehát, ha játszani a rendszert, legalább az egyik a jóslatok van kötve, hogy teljesen igaz. A kártyák száma vásárolt nem lesz túl nagy.
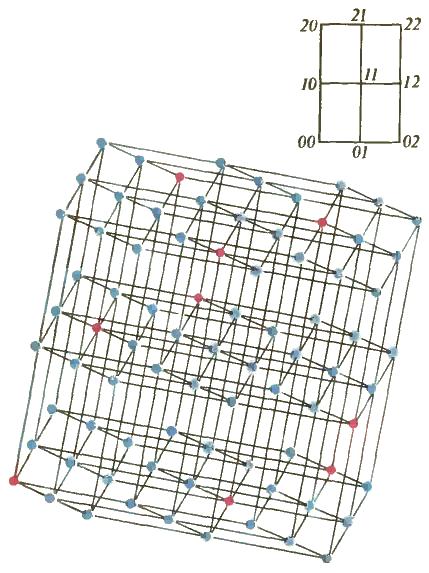
Structure térben E 4 3. A felső ábrán a 9. pont a térben E 2 3. szám számozott 0-8 a terner jelöléssel. Kapcsolódó élek pont „hármas” számok, amelyek különböznek egymástól pontosan egy szimbólum (a pontok a parttól 1). E március 4 nyert E március 2 helyett az egyes pontok a térben E 9 pont március 2; különböző terek számozva „hármas” számok 0 és 8 Enumerate pont minden ilyen terek, valamint a felső ábrán. Ezután a „hármas” számát minden pont E kapjuk április 3-án hozzárendelési pont számra a terek E 3. 2, amelyben fekszik. Az ábra jelölt kilenc pont, hogy tartoznak a rendszer lineáris C0 -.
"Sportprognoz" 4 mérkőzés
Könnyebb lesz megmagyarázni az ötlet épület l-rendszerek a példa a játék a „Sportprognoz-4”, amely felajánlotta, hogy kitalálni az eredmények csak négy játékot. Jelöljük a készlet minden négy-dimenziós vektorok három szimbólum - nullák, is, és kettesével - 4-E-4 3. Méret rendszert ezután egyenlő a száma E elemeit március 4 (= 81). 3. eset rendszer már elgondolkodtató. A probléma csökken a kiválasztás E április 3 részhalmaza C minimális vektorok számát, hogy minden vektor e € E március 4 C megadhatja legalább egy vektor c, e jellemzi legfeljebb egy helyzetben.
Definíció. Hamming-távolsága a vektorok a és b jelentése a különböző alkatrészek számát e vektorok.
Például, a távolság a vektorok a = (0,1,2,0) és b = (0,2,0,0) egyenlő d (a, b) = 2.
Feladat 1. Ellenőrizze, hogy a Hamming-távolság megfelel a háromszög-egyenlőtlenség
Tekintsük a következő C0 rendszert. (0,0,0,0); (1,0,1,1); (2,0,2,2); (0,1,1,2); (0,2,2,1); (1,1,2,0); (2,1,0,1); (1,2,0,2); (2,2,1,0).
Bebizonyítjuk, hogy C0 egy 3-rendszert. Közvetlen ellenőrzés azt mutatja, hogy a távolság közötti bármely két vektor C0 3. A háromszög-egyenlőtlenség a Hamming-távolság létezik vektor e € E 3. 4 távolságban 1 egyidejűleg két a és b vektorok a C0 (egyébként d (a, b) = 2). A készlet vektorok E 4 3. a parttól 4 3 Összesen 81 vektor! Ezért minden vektor E március 4 közé tartozik, az ilyen készletek szükség.
1. példa Vektor (2,1,2,1) tartozik a készlet vektorok, amelyek a parttól 4 3 található a távolból n. a parttól j Cn i * (q-1) i vektorok (Cn I - binomiális együttható egyenlő n / ((n-i) * i) !!!.
8 (Hamming kötött). Bizonyítsuk be, hogy minden kódot
k<=Logq [q n /V(n,t)]
([X] - egész részét x). (3)
Ha a kód paramétereket (3) van egyenlőség, a kód az úgynevezett tökéletes.
Származott mintegy negyven évvel ezelőtt, a matematikai elmélete kódoló most egy fejlett és nagyon mély tudomány. Az ő származása Claude Shannon, a már említett Richard Hamming, Marcel Golay és más tudósok. További információ a kódok, a hibák kijavításával, akkor olvassa el a könyvet Arshinova MN Sadowski LE "kódok és matematika" (Moszkva, "Science", 1983, Könyvtár "Quantum", vol. 30), A. Yaglom Yaglom IM "valószínűség és információk" (M., "Nauka", 1973).
Könnyen belátható, hogy tökéletes l-rendszer egybeesik a tökéletes kódot. Különösen a 3-rendszer játszik mini "Sportprognoz" - egy kódot a q = 3, k = 2 és n = 4, kijavítása egy hiba. A fentiekből következik, hogy a kód egy lineáris (abban az értelemben, a testmozgás 2) és tökéletes, és tartalmaz, ahogy kell, q k = 9 vektorok.
A javasolt 3 fenti rendszer a forgalomba négy mérkőzést lehet általánosítani a „valódi” esetében 13 mérkőzést; ez ad egy 1-12 szénatomos rendszer, amely a 3 10 = 59.049 kártyák. Azt feltételezzük, hogy a vektor x € E3 13 tartozik C1 rendszer. ha a koordináták megfelelnek a következő egyenletek (ismét modulo műveletet 3):
Mint említettük, a vektor kerül hívásra egy sor első kilenc koordinátákat.
Exercise 9. Legyen a számát a vektor x = (x1. X13) € C1 (x1. X10) = (0,1,1,1,2,0,2,1,2,1). Keresse x.
Jóváhagyása. Beépített 12 rendszer lineáris, és tökéletes.
Valóban, hagyja, hogy a vektorok x és y kielégíti (4), akkor x + y 2x és kielégítik az egyenletrendszert. Még több nehéz bizonyítani, hogy a távolság bármely két vektor C1 rendszer nem kevesebb, mint három. Tekintsük két vektor x, y € C1. Ha ezek a számok megegyeznek, akkor x = y. Ha a számok különböznek a három vagy több helyen, akkor készen vagyunk. Hagyja, hogy a számok különböznek egy pozícióban, például i-edik. Aztán figyelmét, hogy az xi (1<=i<=10) входит с ненулевыми коэффициентами в правые части по меньшей мере двух уравнений системы (4), т. е. по меньшей мере две из трёх последних координат векторов x и y будут различными. Если же номера векторов x и y различаются в двух позициях, скажем, i-й и j-к, то для доказательства достаточно показать, что они различаются ещё по крайней мере в одной позиции. Этого может не быть только в случае, когда i-я и j-я переменные в правые части всех уравнений (4) входят с одинаковыми коэффициентами. Проверка показывает, что таких переменных не существует. Итак, доказано, что расстояние между двумя любыми векторами x, y€C1 не меньше трёх. Тогда множества векторов из E3 13. находящихся от x и y на расстоянии <=1, не пересекаются. В соответствии с упражнением 7 каждое такое множество содержит 27 = 3 3 векторов. Общее же количество векторов в системе равно числу различных номеров, т. е. 3 10. а общий объём соответствующих им непересекающихся множеств равен 3 10 *3 3 =3 13. что совпадает с числом всех возможных карточек. Что и требовалось доказать.
Beépített 12 rendszer egy kódot q = 3, n = 13, k = 10, kijavítása egyetlen hiba. Ez a kód - képviselője a család tökéletes Hamming kódok q = 3, n = (3 m -1) / 2, k = n-m.
Térjünk vissza egy kicsit, hogy C0 rendszer mini „Sportprognoz”. Írunk el a kilenc vektorok egy sorban. Törlése a táblázatból bármely oszlop, megkapjuk a rendszer kilenc lineáris vektorok „Sportprognoz-3”. Meg lehet mutatni, hogy ez a rendszer a legjobb között lineáris, azaz. E. Tartalmazza a lehető legkisebb számú kártyát. Kiderült, hogy az elutasítás feltételeit linearitás lehetővé teszi, hogy javítsa a rendszer. Legjobb nemlineáris hossza 3-2 rendszer áll, csak öt vektorok. Itt is van:
* - Tudod, hogy nem lehet javítani.
Kereszt hossza szeptember 11-rendszer
A gondos megfigyelése az asztalra csapott egy csillag, magányos villódzó a közepén. Van egy csodálatos 9-C2 rendszer hossza 11. Az ő története, és az alkalmazás szolgálhat a telek egy érdekes matematikai regény. De először néhány szó a karaktert. Ez egy lineáris rendszer sem tökéletes. Tökéletesség nehéznek bizonyulhat, ha tudjuk, hogy bármely két vektor rendszer a parttól nem kevesebb, mint öt. Ezután, mint korábban, a beállított (729 = 3 6) származó vektorok E3 11 a parttól <=2 от некоторой точки системы, не пересекаются. Поскольку в каждом из этих множеств 243=3 5 векторов, суммарный объём этих множеств совпадает с общим числом векторов в E3 11 .
Adunk a egyenletei a terner számát (x1. X2. X6) bármilyen vektor x, tartozik a rendszer C2. A többi az ő öt koordinátáit:
Amellett, hogy ez a terner rendszer M. Golay művében 1949-ben leírt egy másik lineáris tökéletes rendszer - 20-C3 rendszer hossza 23 vektorokat nullák és egyesek - a kód paraméterekkel q = 2, n = 23, k = 12, 3 fix hiba. Ez a rendszer tartalmazza 2 12 = 4096 vektorok és hasznos lehet a „Sportprognoz” 23 harcol a játék nélkül bárki.
Gyakorlat 11. eredményeit felhasználva gyakorlatok 7. és 8. azt mutatják, hogy a rendszer C3 tökéletes (és ezért tartalmazza a lehető legkisebb számú kártyák ilyen paraméterek közé rendszerek).
A felfedezés, készült Virtakallio, annál is inkább meglepő, hogy a q = 3 más, nem-triviális tökéletes L-rendszerek l<=n-2 ни для каких значений n не существует. При l=n-1 существуют еще системы с параметрами, приведёнными в конце предыдущего параграфа. При q=2 список нетривиальных совершенных систем с l<=n-1 исчерпывается 20-системой C3 и семейством (n-1)-систем с n=2 m -1 и k=n-m. Эти два утверждения следуют из глубокой теоремы о совершенных кодах, доказанной только в начале 70-х гг.
Kapcsolatban felmerülő a Golay kódok C2 és C3 matematikai problémákat, hajlamosak, hogy meglehetősen nehéz. Még a probléma gyors (kimerítő) a megállapítás a nyerő kártya C2 rendszerek jól ismert eredmény forgalomban nagyon nehéz. Kívánja próbálni a kezét ebben a nehéz (bár megoldható) a problémát meg kihasználni az egyenletrendszert (5) jár el és a szellem a gyakorlat a 6. és 9., akkor lehet, hogy nyitott minden új módon oldja meg ezt a problémát?
Az utóbbi probléma, szeretnénk itt érinteni miatt „Sportprognoz” történik, ha egy játékos vállalja, hogy t az n egyezés a minden a három eredmény - a döntetlen, a győztes és vesztes az egyik csapat, és b = nt mérkőzések nyer szinte hihetetlen. (Például egy focimeccsen "Barcelona" (Madrid) - "Star" (Perm), egy csapat lehet a legjobb támaszkodni a sorsoláson.) Jelöljük E2,3 (b, t) több hosszúságú vektor b + t, ahol első koordináta b veszi a értékei 0 vagy 1, és az utolsó t - 0, 1 vagy 2. a C L-vegyes rendszert "Sportprognoz" kell állnia a vektorok E2,3 (b, t), hogy minden vektor egy € E2,3 (b, t) létezik egy c vektor € C, található egy Hamming-távolság nem több, mint l.
12. Mutassuk meg, hogy a távolság <=l от фиксированного вектора a€E2,3 (b, t) находится SUMi=0 l 2 l-i Cb i Ct l-i векторов.
13. Construct 3 rendszer t, b = 2, amely hat kártyák.
Ez már világos, hogy az építési rendszerek „Sportloto” játékok járnak venni egy több vektor a több n E2, W bináris vektorokat tartalmazó, n hosszúságú, pontosan w egységeket. Nem tudjuk, hogy egy jó rendszer a „Sport Lottó”, de akkor kap egy egyszerű egyenlőtlenség, jelezve, hogy minden ilyen rendszernek tartalmaznia kell egy csomó kártyát. Számuk, természetesen,
Ez attól függ, hogy milyen magas a követelményeket a várható nyereség. Mint említettük, számos kártyák úgynevezett D m-rendszert, ha az ebből eredő forgalomból legalább egy ilyen kártyát nyeri szám nem kevesebb, mint m. Tekintsük a „Sport Lottó - 6 a 49-ből.” 6. rendszer tartalmaz C49 D0 = 13.983.816 6 kártya - minden vektor sokaságától származó E2 49,6 bináris hosszúságú vektor 49 hat egység. Mindenesetre D 1-5 rendszerben két vektor C1 és C2 a d (C1, C2) = 2. Valójában bármely két vektor tartalmazó azonos számú egységek egymástól távolságban chotnom. Ezért, ha nincsenek vektorok C1 és C2 úgy, hogy d (c1, c2) = 2, akkor minc1, d c2 (c1, c2) = 4, és van egy vektor, y € E2 49,6. amely a legközelebb van a rendszerben ez a vektor y a parttól 2. Ezután, ha y az eredménye a keringés, a D1 nem fog találni egy olyan kártyát, öt nyertes számokat.
14. gyakorlat (határ Hemmiiga vektorok azonos számú egység).
a) Bizonyítsuk be, hogy a vektorok számát E2 49,6. a távolból <=2s от данного вектора c€E2 49,6. равно
M (s) = Sumi = 0 s C6 i C43 i = Sumi = 6-s 6 C6 i C43 6-i
b) Igazoljuk, hogy | D1 | D1 a kártyák száma a rendszerben 5 - nem kevesebb, mint [C49 6 / M (1)] = 53.992
([X] - a legkisebb egész szám nagyobb vagy egyenlő x-szel).
Hasonlóképpen, azt mutatja, hogy minden D2-4 rendszer tartalmazhat kevesebb, mint 1014 kártyák bármely olyan rendszer-D6 3 - kevesebb, mint 54 kártyákat. A „Sportloto - 5 36» | D1 |> = 2417, | D2 |> = 79, | D6 |> = 8.
Összefoglalva, bemutatunk egy példát egy 2-D rendszer mini „Sportloto”, amely ahhoz szükséges, hogy kitalálni 6 8 számok:
Ennek eredményeként a forgalomban bármely tartalmaz két nulla, létezik egy vektor C € D, hogy egy vektor koordináta, y c és mindkettő tartalmaz nulla. Ezután a távolságot y és c nem több, mint kettő, azaz D - valójában 2 rendszer. Megmutatjuk, hogy a két rendszer egy kisebb számú vektor létezik. Sőt, a három vektor együttesen tartalmazzák összesen hat darab nulla, és akkor is, ha azok különböző pozíciókban, ott marad a két pozíció, amely nem tartalmaz nullák. Elhelyezés azokat a pozíciókat nulla vektor y, azt látjuk, hogy ez található a parttól 4 mind a három vektor rendszer. Ez azt jelenti, 2-F-rendszer 8 optimális hossza.
Műszaki tudományok kandidátusa A. Bargh,
Műszaki tudományok kandidátusa S. Litsyn