Ilyen megoldásokat problémák molekuláris fizika
Ez a probléma könnyen megoldható a használata egyenlete Mengyelejev-Clapeyron
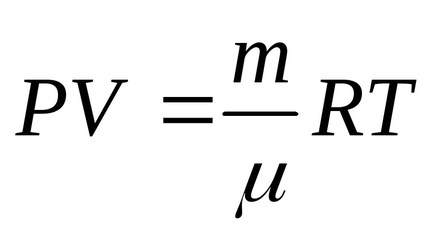
Írd meg, hogy az első állam, a gáz:
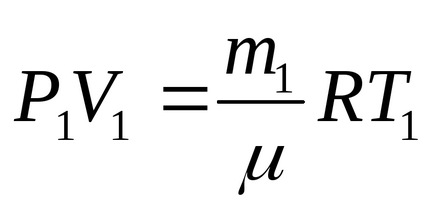
És a második állapot (amikor a részét a kibocsátott gáz):
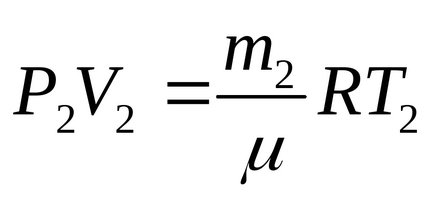
Úgy gondoljuk, hogy a palack mérete megváltozik, ezért a folyamat izochor V1 = V2 = V Vegyük észre azt is, hogy a T2 = T1 -8, AM2 = m1 -0,4m1 = 0,6m1.
Osszuk egyenlet (2) az (1) egyenlet:
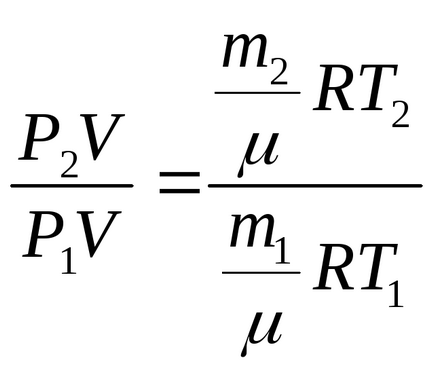
A: A nyomást csökkentjük 1,72 alkalommal.
Oxigén massoym kg = 2 = 1 teljesül obemV1 M3i nyomás P1 = 2,02 ∙ 105Pa. A gázt ezt követően melegítjük állandó nyomáson obemaV2 m3 = 3, akkor állandó térfogaton, amíg P3 = 5 ∙ 105Pa nyomáson. Keresse meg a változás belső energia Au, gázgyári gáz át az A és a számos teplotyQ.
ΔUnahoditsya változni belső energiája a képlet:
ahol μ-moláris tömege oxigén, és izo- száma szabadsági fok. Mivel az oxigén normál körülmények között - kétatomos molekula, tehát i = 5.
Teljes változást a belső energia csak attól függ a különbség a kezdeti és a végső hőmérséklet a T1 és T3. azt találjuk, hogy az egyenlet segítségével Mengyelejev-Clapeyron
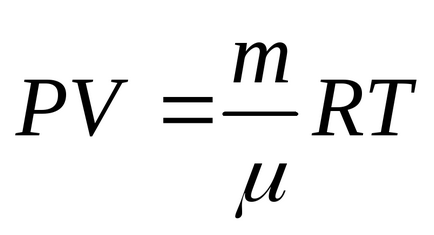
Behelyettesítve (2) megfelelő értékei P és V, megkapjuk értékei hőmérséklet:
Behelyettesítve az (1), a numerikus változók értékei, kapjuk:
Gáz munka egyenlő lesz a gázmennyiség munkák az egyes részekben: A = + Aizob Aizohor. Munka gáz az izochor állapotváltozás egyenlő 0, tehát,
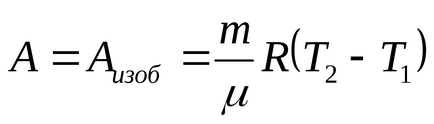
A T2 hőmérséklet található a (2) képletű:
Végezzük el a számítás általános képlet szerinti (3), és így a D érték:
Az első főtétele, az Q hőmennyiség, a keletkező gázok az összege a munka tökéletes gáz és a változás a belső energia Au:
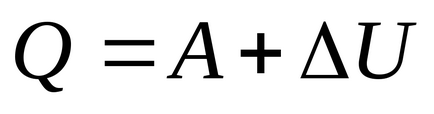
A számítások elvégzése kapjuk: (J).
Válasz: Au = 3,25 MJ MJ A = 0,4, Q = 3,65 MJ.
Thermal gép munkáját végzi Carnot-ciklus. A fűtő hőmérséklet T1 = 230ºS, hűtőszekrény T2 = 300 K, a hűtőszekrény a hőerőgép fűtőelem szolgál egy másik hőerőgép. Néhány a gépek hatékonysága nagyobb, és hányszor, ha a különbség a fűtés és a hűvösebb hőmérséklet mindkét gépen ugyanaz?
Amikor csökkentő a forró fém bár van egy átadása egy hőmennyiség Qmaslu és kaloriméter. Ebben az esetben a sáv hőmérsékletre hűtjük T3. és az olaj, és a kaloriméter melegítjük T3. Feltételezve, hogy a rendszer el van szigetelve a külső hőforrás alkotják a hő egyensúly egyenlet:
ahol Q1 - hőmennyiség adott ki acélrúd, Q2 - hő mennyiségét kapott kaloriméter AQP3 - hő mennyiségét, így olajat kapunk. olaj tömegértékeket a térfogatot és sűrűséget:
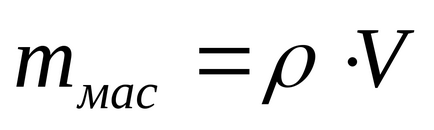
Az (1) egyenlet, figyelembe véve a kifejezéseket Q1, Q2, Q3 és (2):
,
ahol kifejezett SMAS:
.
.
A: A fajhője olaj SMAS = 2 kJ / (kg ∙ K).
Annak megállapításához, a változás az entrópiában ΔSpri izoterm és izobár expanziós nitrogén massoym = 100 g térfogatban 20 l 148 l.
Expression találni az entrópia:
a) Egy izoterm folyamat T = const, így annak vegye ki az integrál jel. Ezután (1) egy izoterm folyamat formáját ölti:
Az izotermikus folyamat
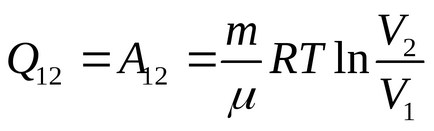
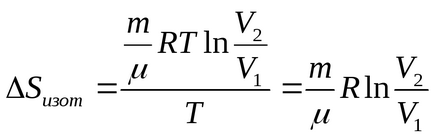
Végezzük el a számítást: (J / K).
b) az izobár folyamat P = const, és
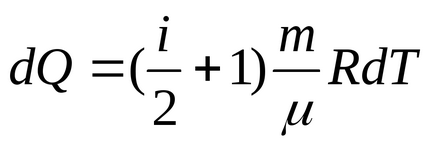
Mivel a hőmérséklet a izobár változás arányában mennyiségének
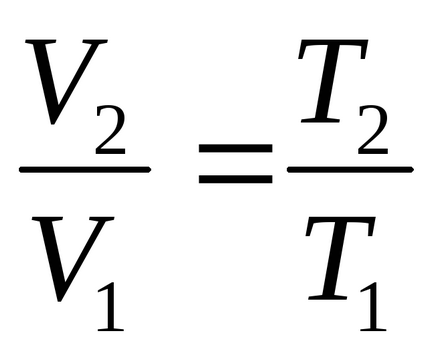
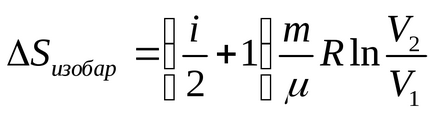
Végezzük el a számítást: (J / K).
A: A változás a entrópia izotermikus folyamat ΔSizot = 59,4 J / K, és az izobár - ΔSizobar = 207,75 J / K.