Bármely két test vonzza egymást, olyan erővel, hogy egyenesen arányos a tömegek a két szerv és
Ez a törvény, az úgynevezett egyetemes tömegvonzás törvénye, a matematikai formában van írva a következő:
ahol m1 és m2 - testsúly, R - a közöttük lévő távolság (lásd a 11 A. ábra ..), és G - a gravitációs állandó egyenlő 6,67.10-11 Nm 2 / kg 2.
A gravitáció törvénye először fogalmazott Newton, amikor megpróbálta elmagyarázni egyik törvénye Kepler, azt állítva, hogy az összes bolygó az arány a kocka a távolság R a Nap a tér a T időszakban forgalomban körül ugyanúgy, azaz
Levezetjük a gravitáció törvénye, mint Newton tette ezt, azt hiszik, hogy a bolygók a körökben. Ezután szerint Newton második törvénye, hogy a bolygó tömege MPL mozgó R sugara a kör v sebességgel és centripetális gyorsulás v2 / R F erőt, felé a Nap (lásd 11B ..), és egyenlő az:
V sebessége a bolygó lehet kifejezni az R sugár a pályára és a keringési ideje T:
Behelyettesítve (11,4) a (11.3) kapjuk a következő kifejezés az F:
Kepler törvény (11,2) következik, hogy T2 = const.R3. Következésképpen, (11,5) lehet alakítani:
Így a nap vonzza a bolygó erővel egyenesen arányos a tömeg a bolygó és fordítottan arányos a tér a távolság közöttük. Formula (11.6) nagyon hasonló a (11.1), hiányzik csak a tömeg a Sun a tört számlálója a jobb oldalon. Azonban, ha az erő a vonzás és a Nap között a bolygó tömegétől függ a bolygó, ez az erő is függeni fog a tömege a nap, és így, az állandó a jobb oldali (11.6) tartalmaz egy napenergia tömb, mint az egyik tényező. Ezért Newton fejlett híres hipotézist, hogy a gravitációs erő függ a termék tömegének szervek, valamint a törvény vált amit felvett (11,1).
Az egyetemes tömegvonzás törvénye és Newton harmadik törvénye nem zárják ki egymást. A képlet szerint (11.1), az erő, amellyel a test 1 vonzza a 2 test egyenlő az erő, amellyel a 2 test felhívja a test 1.
gravitációs erő nagyon kicsi a szervek normál méretű. Így két szomszédos személygépkocsi vonzódnak egymáshoz erővel egyenlő a tömeg esőcseppek. Azóta, mint G. Cavendish 1798-ban határozza meg az értékét a gravitációs állandó, az (11.1) segített, hogy egy csomó felfedezések a „világ hatalmas tömegek és távolságok.” Például, ismerve a értéke a gravitációs gyorsulás (g = 9,8 m / s2), és a sugara a Föld (R = 6,4.106 m), lehetőség van arra, hogy tömegének kiszámításához MH következik. Minden egyes testtömeg m1 közelében a Föld felszínén (azaz R távköznyire a középpontjából) a gravitációs erő hat a vonzerőt egyenlő M1G, amelyben a szubsztitúció (11.1) helyett F ad:
ami azt jelenti, hogy a MH = 6,1024 kg.
Ellenőrző kérdések:
· Fogalmazza meg a gravitáció törvényét?
· Mi a gravitációs állandó?
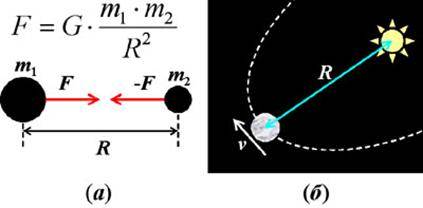
Ábra. 11. (a) - megfogalmazni a egyetemes tömegvonzás törvénye; (B) - a következtetés az egyetemes tömegvonzás törvénye Kepler törvény.
12. § A gravitációs erőt. Tömeg. Súlytalanság. Az első kozmikus sebességgel.