kérdés Newton
A mi előadások
Tegyük fel, hogy egy intervallum (a. B), ahol tudjuk, hogy az f (x) egy szélsőérték és 1 Csakúgy, mint a funkció unimodális és differenciálható.
Newton-módszer - az egyik módszer használatával a származékok. Tény, Newton-módszer ugyanazt a módszert követi az érintők, csak az első deriváltjának.
Construct egy f (x) intervallumban (a. B)
Elbontjuk származéka a Taylor-sor pontban (x 0, f „(x 0)):
Közelítjük. hogy csak az első két tag a sorozat:
Ez azt jelenti, hogy
Így írhat egy rekurzív kifejezést:
Ez a módszer csak akkor alkalmazható, ha a függvény kétszer differenciálható.
Ha az intervallum [a. b] harmadik származék állandó jel, akkor:
Van másodfokú konvergencia (konvergencia a legerősebb), ha az alábbi feltételek konvergencia.
Nincs globális konvergencia (azaz a konvergencia függ a választott kiindulási pont)
Minden lépésnél a módszer kiszámításához szükséges 1yu 2U és származékai.
Az Internet (részlet dokkoló va + + módosítás):
Heurisztikus szempontokról, amelyek a Newton módszert korlátozatlan optimalizálás.
Feltételezve, hogy egy szükséges lépés megoldást találni a problémára
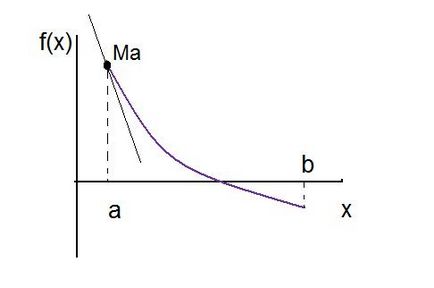
A geometriai értelmezése a képletek (3) és (4) ábrán látható. 10a, és 10b.
Newton-módszert kapcsolatos másodrendű módszerek. mivel minden egyes iteráció kiszámításához ismereteket igényel a második deriváltja az f függvény. Ugyanezen okok miatt, a gradiens módszer utal, hogy a módszer az elsőrendű. Hangsúlyozzuk, hogy nem beszélünk a konvergencia érdekében a módszer és az eljárás által használt származékai funkció van minimalizálható.
Lokalnoysverhlineynoyskhodimosti tétel a Newton-módszer.
Legyen f kétszer folytonosan differenciálható, és x * egy nem degenerált álló pontot. Ezután van egy környéken V x * x pont * úgy, hogy a közelítés (4). kezdeményezett egy tetszőleges kezdeti tochkix 0 ∈ V x *. sverhlineynoskhodyatsya
Igazolás a h a t e l bizonyítási. Nyilvánvaló, F = f „∈ C 1, és ezért
Mivel F „(X *) van nonsingular. A (7) az X elegendően közel X * jelentése nem-degenerált, és az üzemeltető F „(x), és ezenkívül,
Ezért, különösen az X elegendően közel x *
Továbbá, annak a ténynek köszönhető, hogy F differenciálható, és X * - egy álló pont,
X - X * - [F '(x)] -1 F (x) = [F' (x)] -1 F '(X) (X - X *) - [F' (x)] -1 F (x) =
= [F '(x)] -1 [F' (X) (X - X *) - F (X)] = o (x - x *).
x n + 1 - x * = x n - [F „(x n)] -1 F (x n) - x * # 8797;
# 8797; # 966; (x n - X *) = o (x n - X *).
és ezért, x n → x * ha n → ∞. Továbbá, minden q ∈ (0, 1) van # 949;> 0, hogy || # 968; (x - x *) || ≤ q || x - x * || amikor || x - x * || ≤ # 949;. De aztán, ha || x n - X * || ≤ # 949 ;, majd || x n +1 - x * || ≤ q || x n - x * ||. Az utolsó állítás következik nyilvánvalóan szükséges kapcsolatban || x n - X * || ≤ Cq n.
Természetesen, mivel a másodrendű módszer. Newton-módszer igényel nagy mennyiségű számítási munkát jelent, mert ki kell számítani a második deriváltja.
Ha f emellett erősen domború. kijelenthetjük konvergencia, hogy megoldja a problémát (1). és nem csak egy stacionárius pontja f. és ezen kívül, hogy értékelje a sugara a szomszédságában, ahonnan konvergálnak Newton közelítés.
Tétel a másodfokú konvergenciája Newton-módszer.
Legyen f ∈ C 2, sőt, f '' a Lipschitz konstans L. Legyen f erősen vypuklas konstans # 955;. Legyen V x * - szomszédságában a probléma megoldásának (1). álló pontok x ∈ Rm olyan, hogy
Bizonyos alkalmazások jelentős hátránya Newton módszer nagy számítási nehézséget: minden lépésben igényli kiszámításához az üzemeltető (mátrix) f „” (x n), és a (HER) kezelés, amely a nagy méretek Art óIT számításigényes nagyon drága. Az egyik módja annak, hogy megkerüljék ezt a nehézség az, hogy "befagyasztása" az üzemeltető f '' (x n) - segítségével az egyes lépésekben [f '' (x 0)] -1 helyett [f '' (x n)] -1:
A geometrikus értelmezése a módosított Newton-módszer (14) ábrán mutatjuk be. 12.
Belátható, hogy a természetes körülmények között a módosított Newton módszer konvergál csak lineárisan (ez a díj összegének csökkenését a számítás). Egy is fagyasztható az üzemeltető [f „” (x n)] -1 minden, és frissíti azt követően egy bizonyos számú lépést, mondjuk k: