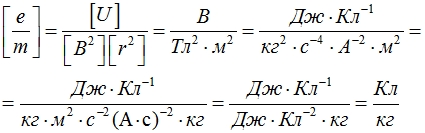Lorentz-erő és annak hatása az elektromos töltés
Elektromos töltések mozognak egy bizonyos irányba létrehoz egy mágneses mezőt maga körül, ami a terjedési sebessége vákuumban egyenlő a fény sebessége, és más környezetben kevesebb. Ha a mozgás a töltés történik a külső mágneses mező, van egy kölcsönhatás a külső mágneses mező és a mágneses mező a töltés. Mivel a villamos áram - arra irányul, mozgását a töltött részecskék, az erő, ami jár, egy mágneses tér áramvezető, lesz az eredménye az egyes (elemi) kényszeríti, amelyek mindegyike alkalmazható elemi töltéshordozók.
A kölcsönhatások a külső mágneses mező és a mozgó töltésekre vizsgált G. Lorenz, amelyek következtében sok a kísérlet adott kiszámításának képlete ható erő egy mozgó töltött részecske által a mágneses mezőben. Ezért az az erő, amely hat a mozgó töltés mágneses mezőben, az úgynevezett Lorentz-erő.
Ható erő a huzal elfolyó (az Ampere törvénye) lesz egyenlő:
Definíció szerint, a jelenlegi egyenlő I = Qn (q - töltés, n - a töltések száma áthalad a keresztmetszete 1 s). Ebből következik:
Ahol: N0 - egységben foglalt térfogatú mennyiségű töltés, V - sebessége mozgásuk, S - keresztmetszeti területe a vezeték. majd:
Behelyettesítve ezt a kifejezést az Ampere-féle képlettel kapjuk:
Ez erő hat az összes díjat a nagy részét a vezető: V = Sl. Töltések száma, vagy az adott kötet lesz:
Ezután a kifejezés a Lorentz-erő fog kinézni:
Ebből arra lehet következtetni, hogy a Lorentz-erő alapján eljárva q töltéssel, ami mozog egy mágneses mező arányos a felelős a mágneses indukció a külső területen, a sebesség és a a szinusz közötti szög V és B, azaz:
A mozgás irányát a töltött részecskék hogy a mozgás iránya a pozitív töltések. Ezért az erő irányában lehet meghatározni a bal kéz szabályt.
Ható erő negatív töltés lesz az ellenkező irányba.
Lorentz-erő mindig merőleges a V-töltési sebesség, ezért a munkájáért. Ez csak a változások irányát V és a kinetikus energia a töltés és az összeget a sebesség ahogy mozog a mágneses mező változatlan marad.
Ha egy töltött részecske mozog mind a mágneses és elektromos mezők, ez lesz egy erő:
Amennyiben E - elektromos mező.
Vegyünk egy kis példa:
Egy elektron gyorsító potenciál-különbség az idő 3,52 ∙ 10 3 V esik egyenletes mágneses mező merőleges a vonalak az indukció. röppálya sugara r = 2 cm, az indukciós területén 0,01 T. meghatározzák a konkrét töltés az elektron.
A fajlagos töltés - az értéke egyenlő az arány a töltés tömeg, azaz e / m.
A mágneses mező B indukciójú a töltés mozog egy V sebessége merőleges vonalak indukciós, a Lorentz-erő hat, Fl = bev. Befolyása alatt a töltött részecske mozog egy körív mentén. Mivel ebben az esetben a Lorentz-erő hatására a centripetális gyorsulás szerint a 2. Newton felírható:
A kinetikus energia, amely egyenlő mV 2/2, az elektron adódó nyereségek működése az elektromos térerősség A (A = Eu), helyettesítve a következő egyenletet kapjuk:
Átalakítása ezeket a kapcsolatokat és eltávolítását bármilyen sebességgel, megkapjuk a képlet meghatározására fajlagos töltésű elektron:
Behelyettesítve a nyers adatokat kifejezett SI, kapjuk: