Ismerje meg az előadó
Ha mozgatja a tollat lecsúszott nyomvonal - a szegmens egy korábbi helyzetben egy új tollat. Ha mozgatja a tollat emelt nyoma sem marad a gépen. A kiindulási helyzetben a toll előadó mindig felmerül, és azon a ponton \ ((0, 0) \).
A parancs a toll, emelje fel a tollat vet előadója. Ha a toll már feloldották, rajzoló figyelmen kívül hagyja ezt a parancsot: nem változik a helyzet a tollat, és nem számoltak be elutasítást. Más szavakkal, bármilyen helyzetében a ceruzát, hogy szüntesse meg a csapatot. Miután ezt a parancsot, akkor lehet emelni.
Ugyanígy, függetlenül az eredeti helyére, miután a csapat letette a tollat, úgy csökken, hogy van, készen arra, hogy dolgozzon.
Fogalmazó rajzok paranccsal át a pontot, és eltávolítja a vektor.
Fordítóból parancs egy pont (a, b) előadója eltolódik egy pont koordinátái (a, b).
Az ábra azt mutatja, az eredmények a parancsok lefordítani a pontot (2, 3) különböző pozíciókban a toll ezt a parancsot.
Úgy látszik, hogy függetlenül attól, hogy az előző toll helyzetét van (2, 3). de a hossza és iránya a szegmens, amely ebben az esetben készült, eltérő lehet.
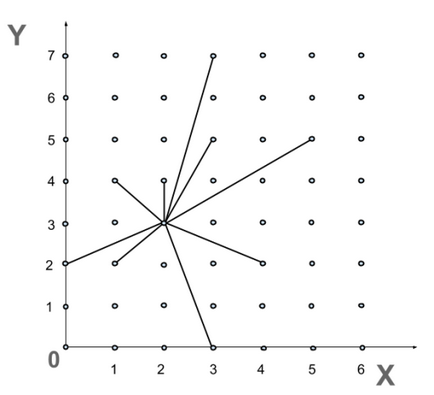
Csapat lefordítani egy pontot az úgynevezett abszolút elmozdulás parancsot.
Nevezze meg a koordinátáit pontok, ahol volt egy előadó lefordítani a parancsot egy pont \ ((2, 3) \).
Ebben az esetben, az eredmény a parancs át a pont \ ((2, 3) \) a különböző kiindulási helyzetek az ábrán látható felhívjuk nem lesz egy szegmens?
Hagyja, hogy a toll előadója a ponton helyezkedik \ ((x, y) \). On parancsot Tolódott-vektor \ ((a, b) \) előadó számít \ (a \) egységek jobbra a vízszintes tengely mentén (abszcissza), \ (b \) egységek mentén felfelé a függőleges tengely (Y-tengely), és mozgatja a tollat pont koordináták \ ((x + a; y + b) \).
Így a megadott koordináták a parancsot, nem számít a származás, és a jelenlegi helyzetben előadója tollat. Tolódott, így a csapat nevezett vektor relatív elmozdulás parancsot.
Az ábra azt mutatja, az eredmények a parancs végrehajtása az eltolt vektor \ ((2, 3) \) különböző pozíciókban a toll ezt a parancsot. Az ábra azt mutatja, hogy a helyzet a toll után ezt a parancsot függ korábbi helyzetét, de ez azt eredményezi, szegmensek, a hossza és iránya azonos.
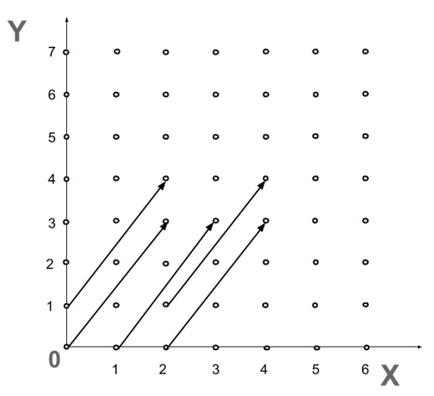
A matematika, irányított szegmensek úgynevezett vektorok. innen ered a neve a csapat.