Turtle egy kört rajzol
Turtle küld a klíring és találkozik egy pillangó. Örülök, hogy vele képet gyűjteménye. De mi a helyzet a szárnyak, amelyek alakú, mint egy kör.
Hogyan kell tanítani a teknős, hogy rajzoljon egy kört? Talán valami hasonló, amit festett? Természetesen. Ne feledje, hogy a képernyőn nézett jobbra 20-gon. Ez nagyon hasonlít egy kört.
1. kérdés: Hogyan készítsünk egy sokszög volt, amennyire csak lehetséges, mint egy kör
Növelheti az oldalak számát. De ahhoz, hogy lakjanak a mi e felek? Korábban már megállapították, hogy az építési kell zárni sokszög Turtle végül visszatért a kiindulási pont, azaz Leírta egy teljes szög 360 fok, és volt ugyanabban az orientációban, mint volt. De a poligon „kínos”, ha az oldalak számát nem elég magas.
2. kérdés: Hány fél kell sokszög tűnt számunkra kört?
Próbáljuk építeni egy szabályos sokszög több párt 360, a „Repeat” parancsot.
3. kérdés Mi az ismétlések számát kell építeni a sokszöget?
Könnyen kiszámítható elfordulási szöge, amellyel a teknős kell fordulnia több mint 1 alkalommal (emlékszem, hogyan kell megszerezni a forgásszög az építőiparban 5, 6, stb szabályos sokszögek) - 1 fok. Milyen hosszú az oldalsó választani? Ha az előírtnál 20 lépés - kör nem fér el a képernyőn, és különben is, ez lesz hangsúlyos a sokszög helyett egy kört.
4. kérdés: Mi az a szám, teknős lépéseket kell tenni, hogy dolgozzon az egyik oldala a sokszög?
1. lépés -A legmegfelelőbb számot. Így az ismétlések száma - 360; oldalhosszúságú - 1 lépés; forgási szög egy ismétlés - 1 fok. Minden ismert rajz egy kör, az első kialakítottunk egy kört. Hívjuk ezt a kört - egy kört a mérete az első. Írunk ezt az eljárást.
EZT OKRUZHNOST1
Ismételjük 360 [VI 1 OL 1]
VÉGE
Egy részét az egyik szárnya kész. Ez könnyű észrevenni, hogy ugyanaz a része van a másik szárnya.
5. kérdés: Mi a különbség?
Elhagyta. Mit kellene változtatni a bal oldali rajz a szárny? Természetesen a forgásirányt. A bal oldali rész fog készíteni az alábbiak szerint:
EZT OKRUZHNOST1_LEV
Ismételjük 360 [VI 1 1 LP]
VÉGE
Most meg kell tanítani a teknős rajzoljon egy kört kisebb OKRUZHNOST1. mert mindegyik szárny két kört. Mi lehet változtatni? Ha megváltoztatja a lépések számát, csak akkor tudjuk növelni őket, de aztán a kör még nagyobb lesz. Próbálja kísérletezni a szög értékét. Nyilvánvaló, hogy ennek csökkentésére nem tudjuk. Mi történik, ha növeli a szög?
Let Angle1 - a szög 1 és 0 UGOL2 - 2 0. Most lássuk, hogyan fog viselkedni, ha a teknős több alkalommal csapatok
[VI PR 1 1] és [VI PR 1 2].
De mielőtt fogjuk ezt a kísérletet, szükséges, hogy megvitassák a következő pont: a teknős fordul át 1 alkalommal szögben 0 és 2 a végén, hogy leírja a teljes szög 360 0.
6. kérdés: Mi az ismétlések számát elég lesz ha a [EP 1 PR 2]? Könnyen kiszámítható, hogy az ismétlések száma egyenlő lesz a 180. Most kezdődik a kísérlet, és látom, hogy a teknős fog viselkedni, amikor végre
Ismételjük 360 [VI PR 1 1] és ismétlődő 180 [VI PR 1 2]
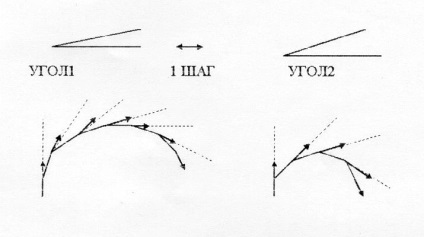
Mint látható, ebben a kísérletben, ha a szög 2 0, akkor hiba kört ír le a kisebb (gondolom az élet, amikor meg kell forgatni nagyobb szögben, ha söpört körbe a stadionban vagy kerek homokozó az udvaron?).
7. kérdés: Milyen következtetést lehet levonni ebből a kísérletből?
Minél nagyobb a forgásszög minden egyes ismétlés, a kisebb kerülete kapunk. Ez azt jelenti, építésére egy második szárnyrésznek (kerülete kétszer kevesebb, mint okruzhnost1) teknős ismétli a parancsot [VI PR 1 2].
Most írjuk be a második eljárást rajz egy kört. Mi ezt a kerülete a második méret.
EZT OKRUZHNOST2
Ismételjük 180 [VI PR 1 2]
VÉGE