Szinusz, koszinusz, tangens, hogy hogyan lehet megtalálni a szinusz, koszinusz és tangens
Az egyik ága a matematika, amely a diákok megbirkózni a legnagyobb nehézséget, a trigonometria. Ez nem meglepő: a szabadon mester ezen a területen a tudás, ez megköveteli a térbeli gondolkodás, a képesség, hogy szinusz, koszinusz, tangens, kotangensét képletek, hogy egyszerűsítse a kifejezést, hogy képes legyen használható értékének kiszámításakor Pi. Ezen kívül, meg kell tudni használni trigonometry bizonyítani tételek, és ez megköveteli a fejlett matematikai memóriát vagy képes megjeleníteni a bonyolult logikai láncot.
Az eredete trigonometria
Ismerete a tudomány kell kezdeni a meghatározása szinusz, koszinusz és tangens, de először meg kell, hogy kitaláljuk, mi általában foglalkozik trigonometria.

A kezdeti szakaszban
Kezdetben az emberek beszéltek a kapcsolatát szögek és fél csak a példa derékszögű háromszög. Aztán kinyitotta a speciális formula, bővül a használatát határok a mindennapi élet ezen ága a matematika.
A tanulmány a trigonometria az iskolában ma kezdődik derékszögű háromszöget, majd a megszerzett tudást a diákok, a fizika és megoldásában absztrakt trigonometrikus egyenletek, a munka, hogy kezdődik a középiskolában.
gömbháromszögtan
Később, amikor a tudomány lépett a következő fejlettségi szint, az alábbi képlet szinusz, koszinusz, tangens, kotangens használták gömbi geometria, ahol különböző szabályok, és az összeget a háromszög szögei mindig nagyobb, mint 180 fok. Ez a rész nem tanítják az iskolában, de tudni a létezéséről kell lennie minimum, mert a Föld felszínét, és a felület bármely más bolygó, konvex, és így bármilyen felületen jegyekkel lesz három dimenziós térben „arc”.
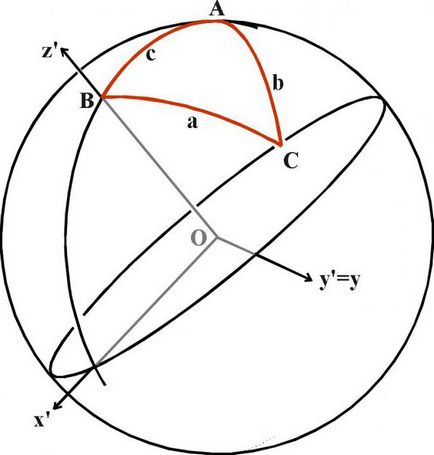
derékszögű háromszög
Kevés módszerek megismerése alkalmazása trigonometria, visszatérünk az alapvető trigonometria további megérteni, mi a szinusz, koszinusz, tangens, egyes számítások is használja őket, hogy végre, és milyen képletben használatra.
Az első dolog, amit meg kell érteni a témához kapcsolódó fogalmakat derékszögű háromszög. Először is, az átfogó - az oldalon szemben fekvő szög 90 fok. Ez a leghosszabb. Emlékszünk, hogy a Pitagorasz-tétel annak számértéke megegyezik a négyzetgyök négyzetének összege a másik két oldala van.
Például, ha a két oldal 3. illetve 4. centiméter, hossza a átfogója 5 cm. By the way, még az ókori egyiptomiak ismerték négy e és fél ezer évvel ezelőtt.
A fennmaradó két fél alkotnak derékszög, az úgynevezett lábak. Ezen kívül, meg kell emlékezni, hogy az összeget a háromszög szögei a derékszögű koordináta-rendszerben egyenlő 180 fokkal.
meghatározás
Végül egy szilárd megértése geometriai bázis, akkor olvassa el a meghatározása szinusz, koszinusz és tangens.
Sine a szög az arány a másik lábát (m. E. szemben lévő kívánt szög) a átfogója. Koszinusza a szög az arány a szomszédos láb a átfogója.

Végül, a szög tangense az aránya az ellenkező oldalon a szomszédos. Ugyanezt az eredményt ad a szétválás a szinusz és a koszinusz-. Lásd: a következő képlet szerint, elosztjuk a hossza a átfogója oldalon, majd osszuk el a hossza a második oldalon, és megszorozzuk a átfogója. Így megkapjuk az arány megegyezik a meghatározása az érintő.
Kotangensét, külön-külön, az arány mellett a sarokban, hogy az ellenkező oldalon. Ugyanezt az eredményt úgy kapjuk meg az egységet a tangens.
Tehát, megnéztük a meghatározása, hogy mi a szinusz, koszinusz, tangens és kotangens, és tehetünk a képleteket.
A legegyszerűbb képlet
A trigonometria képletek nem nélkülözheti - hogyan lehet megtalálni a szinusz, koszinusz, tangens, kotangens nélkülük? De ez az, amit szükséges, hogy megoldja a problémákat.
Az első formula, amit tudnod kell, tanul trigonometria, azt mondja, hogy a négyzetének összege a szinusz és koszinusz az a szög egyenlő eggyel. A képlet az egyenes következménye a Pitagorasz-tétel, de időt takaríthat meg, ha azt szeretné tudni, hogy a szög, nem a párt.
Sok diák nem emlékszik a második formula is nagyon népszerű megoldásában iskolai problémák: egységek mennyisége és szögletes tangense egyenlő egy négyzetének hányadosa a koszinusz a szög. Tekintse meg közelebbről: ez az állítás, mint az első képlet, csak a személyazonosságát a két fél osztottuk a tér a koszinusz. Kiderült, hogy egy egyszerű matematikai művelet nem trigonometrikus képlet teljesen felismerhetetlen. Ne felejtsük el, hogy tudjuk, mi a szinusz, koszinusz, tangens és kotangens, transzformációs szabályokat, és néhány alapvető képleteket, akkor mindig hozza magát szükség bonyolultabb képleteket egy darab papírra.
Térsarok képlet és kívül érvek
További két képlet van szükség, hogy megtanulják, társított értékek, a szinusz és koszinusz értékek összege és különbsége a szögek. Úgy mutatja be az alábbi ábra. Vegyük észre, hogy az első esetben mindkét alkalommal szorozva szinusz és koszinusz, a második áll páros termékek szinusz és koszinusz.
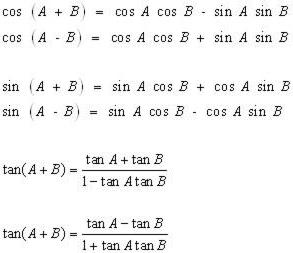
Végül, vegye figyelembe, hogy a képlet a kettős szög lehet alakítani úgy, hogy csökkentse a mértékét szinusz, koszinusz, tangens alfa.
A két alapvető tételek tövénél trigonometria szinuszszűrők tétel és a tétel a koszinuszok. Segítségével ezek tételek, könnyen kitalálni, hogyan lehet megtalálni a szinusz, koszinusz és tangens, ezért a terület a figura és a mérete minden oldalról, és így tovább. D.
Sine tétel azt állítja, hogy ennek eredményeként a választóvonal a hossza mindkét oldalán a háromszög a nagyságát az ellenkező irányból, megkapjuk ugyanazt a számot. Továbbá, ez a szám egyenlő lesz kétszerese a sugara a körülírt kör, azaz. E. A kör, amely az összes pontot a háromszög.

Hibák miatt gondatlanság
Még tudja, mi a szinusz, koszinusz és tangens, könnyű hibázni, mert a szórakozottság vagy hibák egyszerű számításokra. Annak elkerülése érdekében, az ilyen hiba, mi megnézzük a legnépszerűbb közülük.
Harmadszor, ne keverje össze az értékeket a szögek 30 és 60 fok szinusz, koszinusz, tangens, kotangens. Megjegyzés ezeket az értékeket, mert sinus 30 fok egyenlő a koszinusz 60, és fordítva. Ezek könnyen összetéveszthető, így elkerülhetetlenül kap a rossz eredmény.
kérelem
Sok diák nem siet, hogy indítsa el a tanulmány trigonometria, mert nem értik az általa alkalmazott értelemben. Mi a szinusz, koszinusz, tangens, hogy egy mérnök vagy egy csillagász? Ez a koncepció, amellyel ki tudjuk számítani a távolságot a távoli csillagok, előre őszén a meteorit, küldjön egy kutatási szonda egy másik bolygóra. Nélkülük nem lehet építeni egy épületet, hogy tervezzen az autó, kiszámítja a terhelést a felület vagy tárgy mozgás pályáját. És ez még csak a legnyilvánvalóbb példa! Valójában trigonometria egyik vagy másik használják mindenhol, a zene gyógyszert.
Összefoglalva
Szóval, tudod, mi az a szinusz, koszinusz, tangens. Akkor használja őket számítások és sikeresen megoldja az iskola problémát.
Hogyan lehet megtalálni a szinusz, koszinusz, tangens az ismert hossza a lábak, vagy az átfogó, most már tudod. Mivel ezek a kifejezések nem csupán az arány, és az arány - a frakció, a fő cél a trigonometrikus probléma lesz találni egy normális egyenlet vagy a gyökereit egyenletek. Itt segít a hétköznapi iskolai matematika.
