Grafikus módszer minimalizálja - Karnaugh térkép - stréber

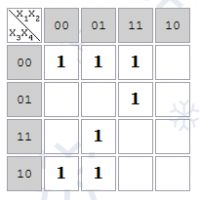
Karnaugh térképek minősülnek megfelelően átépítették igazság táblázat funkciót.

Térképek Carnot - meghatározás lapos söpörni n-dimenziós logikai kocka.

Épített igazság táblázat működésének egy bizonyos módon. Minden cella a táblázat megfelel egy meghatározott felső logikai kocka. Nulla értékek nem kerülnek rögzítésre.

Karnaugh térkép funkció a 4 változó:

Karnaugh térképen tekinthető a felülete az ábrán úgynevezett tórusz ( „fánk”).

p-sejtek - Karnaugh térképet cellában, amely a függvény értékét egység.

Közeli szettek - készletek, amelyek csak egyetlen érv (egy pálya).

Bármely két szomszédos készletek a Karnaugh térkép megfelelő a szomszédos sejteket.

Két szomszédos p-sejtek a Karnaugh térkép implicant így az első helyezés. Például, a sejteket 1100 és a 1101 különböznek csak a változó értéke x3. Ezért adnak implikantu1 24.

Két szomszédos implicants alkotnak implicant első helyezés a második helyezés.

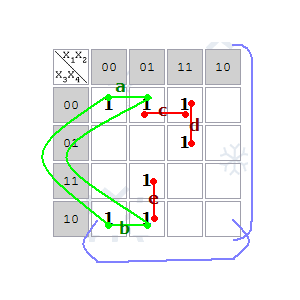
Ezen a térképen, a szomszédos sejtek alkotnak implicants a, b, c, d, e. Így implicants az a és b a szomszédos, így alkotnak implicant második helyezés.

Ha a funkció 5 változók, húzott 2 Karnaugh térkép: az x5 = 0 és X 5 = 1. Ha a 6 változók - 4 lapot úgy, hogy a szomszédos térképek szomszédos cellák azonos koordinátákat:

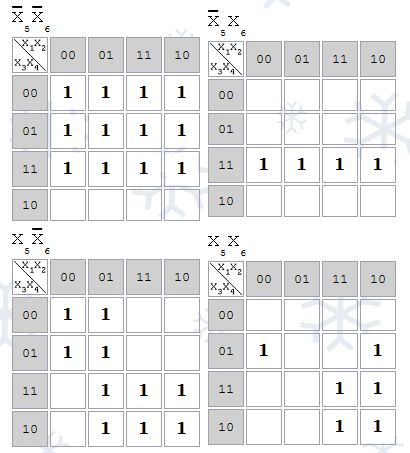
P-szomszédos cellák megfelelő implicants egy kompakt csoportot.

Száma p-sejtek egy kompakt csoport kettő valamely hatványa.

A probléma minimalizálása a kapcsolási funkció segítségével Karnaugh térképek áll megtalálásában implicants magasabb rangú (megfelel kompakt csoportok legnagyobb mérete), amely a p-sejtek a legjobban működik.

Ha Karnaugh térképek jelölje ki az összes kompakt csoportok legnagyobb mérete, a megfelelő diszjunkcióját kötőszavak lesz SkDNF.