Algoritmus Monte Carlo

Metropolis módszer képviselte, mint egy Markov folyamat, amelyben a bolyongó van kialakítva, hogy a valószínűsége, hogy egy bizonyos ponton arányos Boltzmann tényező. Nagyon sok módja van, hogy össze egy bolyongás. E rendszer szerint a rendszer Metropolis:

Véletlenszerűen kiválasztott részecskéket számítjuk, és annak az energia U ().

A részecske mozog egy rövid távolságra a R „= R + Δ véletlenszerű irányba. Ez ahhoz vezet, hogy a változás potenciális energia egy bizonyos összeget Au. Részecske energia most U ().

Kitelepülõ elfogadott valószínűséggel

. ()

Van többféle mozgások MV módszer [9]:

Forgatás körül a molekula véletlenszerűen kiválasztott tengely;

Kötet változás (Gibbs együttes és az NPT);

Mozgó molekulák az egyik cellából a másikba (Gibbs ensemble);

Megsemmisítése meglévő molekulák vagy a bevezetése egy új molekula (Large kanonikus sokaságon);

Növelése bármely molekula (a rugalmas molekulák);

Flip, azaz forgási tengelye körül egy atom által alkotott közvetlen szomszédai (rugalmas molekulák);

Reptation, azaz eltávolítása egyik végét a molekula és a növekedés a másik végén (a rugalmas molekulák);

Permutáció, azaz az eltávolítása egy molekula, és a helyiségeket egy másik molekulát a helyét;

Forgatás a molekula körül egy atom (rugalmas molekulák);

Mindezek a mozgalmak kell venni minden lehetséges konfiguráció egy adott együttesre, valamint minden lehetséges irányait, rendeletek és belső szerkezetek. A 2. ábra mutatja az összes lehetséges elmozdulását a Gibbs együttest.

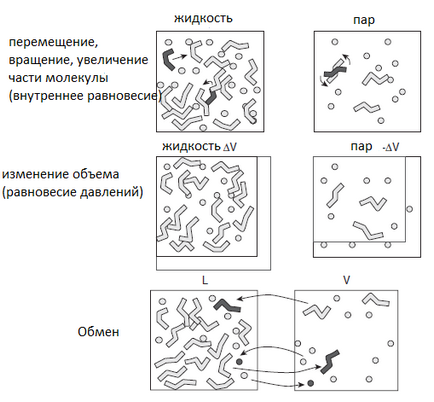
2. ábra alapelvei a Gibbs együttest. Két szimulált sejteket használják, hogy képviselje a fázisok egyensúlyi. Belső mozgás (fordítás, forgatás és zoom) arra használjuk, hogy egy termikus egyensúly állandó hőmérsékleten. A kötet változás eléréséhez alkalmazott nyomás egyensúlyi, és a cseréje molekulák fenntartására használják kémiai egyensúlyt a két fázis között [9].

statisztikai ensemble

Statisztikai együttese egy fizikai rendszer egy sor minden lehetséges állapot a rendszer megfelel bizonyos feltételeknek. Válogatás statisztikai együttest molekuláris modellezés elsődleges kulcs és a nyomaték. Leegyszerűsítve, a kiválasztott statisztikai ensemble rendszer úgy véli, lehetséges állapotok együtt bizonyos korlátozásokkal (állandó hőmérséklet, a részecskék száma, nyomás, stb.) [19]. És azokat a lehetőségeket, amelyek nem követtek el, tapasztalt ingadozásokat. Statisztikai ensemble használjuk a molekuláris modellezés, táblázatban foglaljuk össze 1. Amint az a táblázatból látható, célok alapján, a kiválasztott vagy más statisztikai együttest. Minden statisztikai együttest jellemzi egy valószínűségi sűrűség, azaz előfordulási valószínűséget minden állapot a rendszer együttesen.

1. táblázat Statisztikai részegységeket a molekuláris modellező [9].

Tekintsük a kanonikus sokaságon. megfelel egy fizikai rendszer, amely cserél energiát a környezetet, míg termikus egyensúlyban. Ebben az esetben, az állandó paraméterek a térfogat, a hőmérséklet és a részecskék száma. partíciós függvény

ahol - a termikus de Broglie hullámhossz. A megoszlási hogy annak a valószínűsége, hogy megtalálják konfiguratsiyupodchinyaetsya eloszlás:

Ez a két egyenlet - alapanyagok modellezésére a kanonikus sokaságon.

Modellezése kanonikus sokaságon az alábbi séma szerint:

Véletlenszerűen kiválasztott részecskéket számítjuk, és az energia az ezt a konfigurációt, U (0).

Egy részecske mozog egy véletlenszerű távolság,

,

ahol - a maximális elmozdulás. Az új konfiguráció oboznachaetsyani annak energiyaU (n).

Mozgó elfogadott valószínűséggel:

.

Energia ingadozik, azaz a készlet tartalmazza a rendszer állapotáról eltérő energiákkal. Azonban, ki tudjuk számítani az átlagos energia (gdem - állapotainak száma a ensemble a rendszer), amely össze lehet hasonlítani kísérleti adatok, például útján moláris energia:

ahol - Avogadro számát, N - teljes száma részecskék a rendszerben.

Isotherm - izobár ansamblNPT. ahol a nyomást állandó értéken tartjuk, ahelyett, hogy térfogata. Ezt a szerelvényt gyakran használják, mivel a legtöbb kísérleteket végeznek szabályozott nyomás és hőmérséklet. Tegyük fel, hogy rassmatrivayutsyaN azonos atomok. A partíció függvény:

A kiválasztás történhet a szabály alapján:

).

Egy részletesebb leírás található a [17].

A fent említett szerelvények van állandó részecskék száma, de néha szükség van, hogy információkat szerezzen az átlagos száma részecskék függvényében a külső körülmények, így például, a tanulmány az adszorpciós a porózus szilárd anyagok,. Ilyen célokra célszerű használni nagykanonikus ensemble (BKA). ahol az állandó paraméterek a hőmérséklet, a térfogat és a kémiai potentsialμjj első típusú molekulák. Ehhez együttes partíció függvény formájában:

Egy ennek megfelelő valószínűségi sűrűség:

.

Annak a valószínűsége annak, hogy a mozgás:

.

A részecske kerül egy véletlenszerű helyzetben vagy véletlenszerűen kiválasztott részecske eltávolítjuk. szemcseképző elfogadott valószínűséggel:

,

és eltávolítjuk a részecskék veszik valószínűséggel

.

Így minden mikroállapot jelentése szimulált tartalmazó sejt porózus anyagot elemeztük, és a konfiguráció az adszorbeált molekulák opredelyaemuyuT iμ. Ilyen körülmények között a BCA lehetővé ingadozhat energiasűrűség, és így van a mikroállamok minta, megszámláljuk, és az átlagértékeket ingadozó paraméterek. A kapott adszorpciós izoterma egy telek sűrűségű (vagy átlagos száma adszorbeált molekulák) a kémiai potenciál állandó hőmérsékleten. Generation mikroállapotok alapul Markov folyamat, azaz, bármely adott molekuláris konfiguráció következők által generált véletlen felvétel, törlés vagy mozgása az adszorbeált molekulák. Ha a molekulák nem gömb alakú, akkor minden mozgást kíséri véletlenszerű rotációs [20] .Ansambl leggyakrabban használt kiszámításához a fázis egyensúlyi paraméterek etoansambl Gibbs [21]. Ebben az esetben a két fázist bemutatott két különböző szimulált sejtek. Két módszer modellezés: állandó teljes térfogata a két fázis vagy állandó nyomás. Ugyanakkor állandónak tekinthető hőmérséklet és a részecskék száma. Ha figyelembe vesszük a tiszta együttese használt rendszerek állandó térfogaton, ahol a kimeneti adatok lehetnek a telített gőz nyomása, a párolgási entalpia, vagy a folyadék sűrűsége és gőz. A keverékek esetében Gibbs ensemble lehet használni, mint az állandó nyomáson és állandó térfogaton. Mindkét esetben, az egyensúlyi készítmények fenntartását, és a sűrűsége a molekuláris rendszer egymás mellett faz.Energiya

Jól ismert, az energia egy molekuláris rendszer tartalmaz egy K kinetikus energiával és potentsialnoyU. A molekuláris dinamikai megoldást az egyenleteket a mozgás minden pillanatban lehetővé teszi számunkra, hogy meghatározzuk a kinetikus energia az egyes időpontokban, és átlagolt mozgási energia határozza meg a hőmérséklet a rendszer. A Monte Carlo szimuláció hőmérséklet állandó, és a kapcsolatot a kinetikus energia kiszámítására használják fel a mozgási energia hozzájárulása az együttest. Mindkét esetben fontos, hogy kiszámítja a potenciális energiája a molekulák a koordinátákat. Potenciális energia áll két részből áll: az intramolekuláris és intermolekuláris. Az intermolekuláris potenciális energia, viszont áll egy Lennard-Jones energia, elektrosztatikus energia és polarizációs energia. Az energia a Lennard-Jones uralkodó feszültséget a kis polaritású rendszerek, mint például alkánok (általános formuloySnH2n + 2) a formája:

ahol - a távolság a hatalmi központok. Paraméterek Lennard-Jones potenciális energia a 2. táblázatban ismertetett.

Modell potenciális energia foglalkozni az egyes atomok, mint a hatalom központja a Lennard-Jones, az úgynevezett „AllAtoms” vagy „összes atom” [22. 23. 24]. Ha az erő központja néhány atom, atomcsoport, akkor ez a modell az úgynevezett „UnitedAtoms” vagy „kombinált atomok” [25. 26. 27]. A harmadik modell „AnisotropicUnitedAtoms” vagy „kombinált anizotrop atomok”, lehet, hogy erő központ közötti térben egy csoportja az atomok (3. ábra) [28 29] .Elektrostaticheskaya energia határozza meg a kifejezést:

, ahol az összegzés van az összes lehetséges pár molekulák Q töltésű távolság választja el egymástól, -elektrostaticheskaya állandó.

A polarizációs energia miatt deformációja az elektron felhő körülvevő molekulák által a poláris molekulákat, vagy szilárd anyagok. Általában a számításokban ez úgy értendő, hogy ez az energia közvetve figyelembe veszik az energia a Lennard-Jones vagy elektrosztatikus energiát.

Az energia az intermolekuláris kölcsönhatási energia áll nyújtás, hajlító és csavaró. Stretching annak köszönhető, hogy a változás kötést L hossza. sgib- uglaθ a változás a két kötés és diéderes kruchenie- váltással uglaφ (4. ábra).

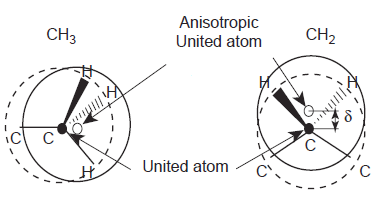
3. ábra elve intramolekuláris potenciális Anizotropikus Egyesült atomok (AUA), valamint a kapacitás Egyesült atomok (UA). Az első esetben AUA erőt Center közelében található a geometriai középpontjában a rendszer, a második esetben AU erő központ található, a sejtmagban szénatomok [9].

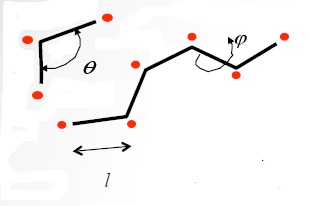
4. ábra paraméterek flexibilis molekulák

Ezek a potenciális energia alapján számítják ki az alábbi képletek:

energia hajtási él (32)

torziós energia, (33)

és szakítási energia kiszámított Lennard-Jones potenciál (Formula 44)

Ha a molekula flexibilis, akkor a összegzése valamennyi sarkok és hatalmi központok párok elválasztott több mint három kötéssel. Ha a molekula tekintjük merev, ezek a hozzájárulások nem veszik figyelembe a számítási folyamathoz. Azt is meg kell jegyezni, hogy ahelyett, hogy a kifejezések (45) és (46) fel lehet használni, és mások, és a fő ok, amiért a (45) és (46) - az, hogy kiszámításakor azt az időt kevésbé számítógép [30 31].

 /