gazdaság Gysin
Tegyük fel, a keresleti függvény Qd = 100 -P, és a funkciót
kínál Qs = 2 - P - 50, ahol p - az az ár rubel,
érték Qd kereslet és predlozheniyaQs ezer darab.
a) Határozza meg az egyensúlyi árat és az egyensúlyi mennyiséget.
b) Ha a kormány úgy dönt, hogy csökkentse az árat 40 rubelt,
célja, hogy ösztönözze a fogyasztói, hova vezet? Határozzuk
értékét a kereslet és kínálat, ha van túlzott
ajánlat (túltermelés, túltelepítés) vagy túlsúlyos
kereslet (deficit), mi a fogyasztás mértéke?
Pont az egyensúly az állami beavatkozás a munka
Ezen a piacon megtalálható a következő egyenlet:
Ha a kormány csökkenteni fogja az ár 40 rubelt. az összeg a kereslet
eléri a 60 (qd = 100 - 40 = 60), de kínálnak csökkentett
30 (Qs = 2-40 - 50 = 30). Van túlkereslet 30
az azonos mennyiségű értékesítési: Q = min (qd, Qs) = 30.
Funkció a kereslet-kínálat van beállítva: Qd = 200- 4-R
és Qs = 6 • P - 100, más néven fajlagos költségek
C = 25, amelyek függetlenek a termelési volumen. Összehasonlítás
Az értékesítési volumen egyensúlyi ár és az ár, amely maximalizálja
teljes nyereségének a gyártók az iparban. Hogy a következtetést,
Ezért az állam nem ajánlott, hogy beavatkozzon a piac
Találunk a lényeg az egyensúly: P0 = 30, Q0 = 80, Zener> P0
értékesítés határozza meg a keresleti függvény, míg P <Р0 —
javaslatokat. Meg kell találni az ár P”, ami meghatározza a maximális
profit, persze, ha R> C:
- at (P - 25) - (200-4-F) = - 4 + 300-P2-P - maximális 5000
születik a P pont, és egyenlő az 75/2 = 625;
- at (P - 25) - (6-R - 100) és 25 <Р <30 максимум
érhető el, ha a P = 30, és a 400.
Ezért optimális termelők
ár P = 37,5, ami számukra a legnagyobb nyereség $ 625
Ábrázoljuk a kereslet, uborka javaslat táblázatos adatokat.
A válasz a kérdésre:
ha az ár változik uborka 2 den.ed / kg és 2,5 pénzegység / kg, akkor hogyan kell változtatni a mennyiséget követelt?
Határozza meg az egyensúlyi ár 1 kg uborka és az egyensúlyi mennyisége uborka.
Ábrázolási kell halasztani a lényeg a kereslet (kínálat) a koordináta sík és a csatlakoztatáshoz.
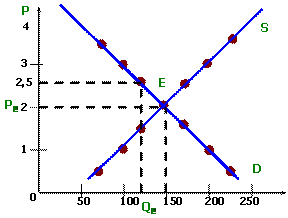
ha p = 2 den.ed, QD = 150 kg;
ha P = 2,5 den.ed, QD = 125 kg (a táblázatos adatokat), 150-125 = 25 kg. Nagysága a kereslet csökkent 25 kg;
egyensúlyi ár és a mennyiség határozza meg a táblázatban előírt QD = QS. PE = 2 de.ed, QE = 150 kg. A grafikonon az egyensúlyi ár és az egyensúlyi mennyiség megfelel a metszéspontja a grafikonok a kereslet és kínálat (PE, QE)
Feature javaslatokat marhahús formájában: QD = 30 - P, ahol QD - az értéke kereslet a marhahús naponta (kg), és a P - az ár kilogrammonként. ajánlatok funkció leírása a következő egyenlet: QS = 15 + 2P, gdeQS - szállított mennyiség naponta (kg).
konstrukció grafikonok a kereslet-kínálat;
Keresse az egyensúlyi ár és az egyensúlyi mennyiségének hús;
milyen helyzet áll elő, a húspiac, ha az ár van beállítva 3 pénzegység per kg? Problémák algebrai módszer;
ha a javaslatot, hogy csökkentsék 60% -kal minden egyes ár szinten, ez hatással lesz az egyensúlyi mennyiség és az egyensúlyi ár?
megtalálják a rugalmasság a kereslet-kínálat egyensúlyi pont.
1. A kereslet és a kínálat egyenlet - az egyenlet lineáris függvények, annak érdekében, hogy őket építeni kell tudni a két pontot.
F = 0, QD = 30; QD = 10, P = 20 a keresleti ütemezés
F = 0, QS = 15; QS = 20, P = 2,5 az gráf predlozheniya.Sm. Glavu6. Funkciók és grafikonok.
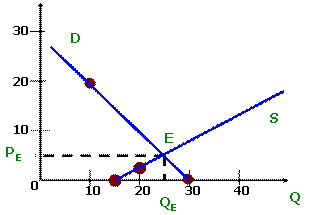
2. A grafikon az egyensúlyi ár és az egyensúlyi mennyiség megfelel a metszéspontja a kereslet és kínálat grafikonok E (PE, QE). Nagyon gyakran, grafikus módszerrel, akkor meg a közelítő érték, ezért a legjobb, ha egy algebrai módszer: egyensúlyi állapot: QD = QS vagy PD = PS így:
3. A grafikus módszer: az F = 3 pénzegység QD = 27 kg, QS = 21 kg, a termék hiány 27-21 = 6 (kg).
Algebrai módszer: helyettesítő a kereslet-kínálat egyenlet P = 3 pénzegység
4. kínálat csökkentése 60% -a tekinthető minden egyes ponton a grafikonon. Ehhez hozzon létre egy táblázatot az értékek.
2. Konv árrugalmassági által meghatározott erősítés Q / Q növekmény P / P. Az együttható számított ár rugalmassági modulus, azaz tart egy pozitív értéket.
Ha megváltoztatja az árak 2,1-1,8 E = 10/10 * 2,1 / 0,3 = 7
Amikor az ár változás 1,8-1,5 E = 10/20 * 1,8 / 0,3 = 3
Ha megváltoztatja az árak 1,5-1,2 E = 10/30 * 1,5 / 0,3 = 1,7
Amikor az ár változás 1,2-0,9 E = 10/40 * 1,2 / 0,3 = 1
Amikor az ár változás 0,9-0,6 E = 10/50 * 0,9 / 0,3 = 0,6
Amikor az ár változás 0,6-0,3 E = 10/60 * 0,6 / 0,3 = 0,3
10 20 30 40 50 60 70 Q
Ez az adatokból látható a probléma, hogy a maximális értékesítéséből származó bevételek 48 den. egység tényező. ahol a rugalmasság értéke 1, és a menetrend változás bevételt megerősíti ezt.
Változó ceteris paribus