Végtelenül mély lyuk

Home | Rólunk | visszacsatolás
A legfontosabb példák részecske mozgás a potenciál zsebeket a mozgás a nukleonok a magok, elektronok atomok és molekulák. Basic törvények a mozgás a véges részecskék vizsgálhatjuk például, amikor az alak a lehetséges csökkentése formáját ölti egy négyszögletes végtelenül mély kút szélessége a. A (0, a), a potenciális energia a feltételezett érték nulla, és ez a végtelenbe (ábra. 2.1) kívül van az intervallumon. Ennek eredményeként a részecskék állásfoglalásra nem lép túl a szegmens (0, a) vagy, mint mondják, a részecske egy végtelenül mély potenciálgödör szélessége a.
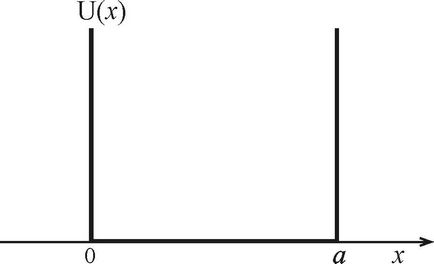
Ábra. 2.1. Négyszög végtelen mélységű potenciálgödör
Mivel a valószínűsége, hogy egy részecske végtelenül mély potenciálgödör egyenlő nullával, akkor a hullám a függvénye a (0, a) egyenlő nullával. Így megkapjuk a peremfeltételek az oldatot a Schrödinger egyenlet:
Mivel a potenciális energia U (x) független az időtől, kiszámításához hullámfüggvényeinek részecskék megoldásához szükséges egydimenziós Schrödinger-egyenlet stacionárius nulla potenciál alján a gödör. azaz
Adunk egyenlet (2) a kanonikus formában:
egy mennyiség dimenziója a hullám száma: m - 1. A jellegzetes egyenletnek összetett gyökereit. Az általános megoldás a differenciálegyenlet (3) felírható
A stacionárius Schrödinger egyenlet, mint ismeretes, tartalmaz egy oszcilláló frekvencia időtényező
. ()
Az első tag a „csökkenő” de Broglie hullám amplitúdója A. hullámszám és gyakoriságát. és a második tag - „a visszavert” de Broglie hullám, azaz hullám terjesztő az ellenkező irányba. Ezek a hullámok koherens, mert ugyanazon a hullámhosszon. Általában lapos de Broglie-hullámhossza nélkül rögzítjük időtényező, azaz formájában (5).
Behelyettesítve az oldatot (5) a peremfeltételek. Van és alkalmazzák Euler formula. megkapjuk
ahol - a normalizálótényező, amelynek kiszámítása a normalizáció állapotban. Behelyettesítve (6) a normalizálás állapotban
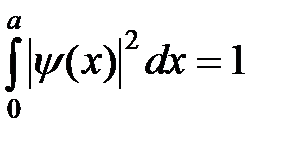
Most helyettesítheti a megoldást (6) a második peremfeltétel és beszerzi. ahol n természetes számok. Így a hullám száma k - a kvantált, azaz kap diszkrét értékrend
Behelyettesítve (7) be (6) végre megkapjuk a hullám leíró függvény állapotban a részecske egy végtelenül mély kút szélessége a potenciál is:
Ahhoz, hogy a spektrum energia a részecske eredmények a helyettesítési értékeket hullámszám (7) a (4) képletű:
Mint látható, az oldatot (8) egy állóhullám de Broglie, amely alakult, mint az interferencia eredményeképpen a „csökkenő” és a „visszavert” koherens de Broglie hullámok által meghatározott kapcsolatban (5) vagy (). Feltétel kialakulásának állóhullám (7) felírható szempontjából a de Broglie hullámhossz figyelembe véve, hogy. akkor megkapjuk
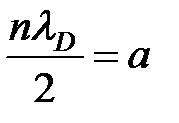
azaz álló hullám keletkezik a feltétellel, ha a pit szélesség egész számú fél hullámhossz egyenlő a kvantum n számot. Annak a valószínűsége, sűrűség, azaz a a valószínűsége, hogy a részecske egységnyi intervallumot a gödör, rendre
Ábra. 2.2 bemutatja a részecske és hullám megfelelő funkciókat az első valószínűségi állapotsűrűség n = 1,2,3, és n = 20 >> 1.
Nyilvánvaló, hogy a kis kvantum számokat, a valószínűség-eloszlást, a részecskeméret a jól erősen nem lineáris, de a növekedés a kvantum a sűrűségfüggvény általában nagyobb egyenletes a határ nagy kvantum számokat. amely megfelel a korlátozó átmenet a klasszikus probléma. Valóban, nagy kvantum-szám n >> 1, hullámhossza a részecske lesz sokkal kisebb, mint a gödör szélessége <<а. что соответствует условию применимости классического описания, в котором волновые свойства частицы не учитываются. В тоже время квантовомеханическое описание используется в случае соизмеримости длины волны де Бройля частицы и характерного размера системы, ограничивающего движение частицы (ширины ямы), что соответствует случаю малых квантовых чисел.
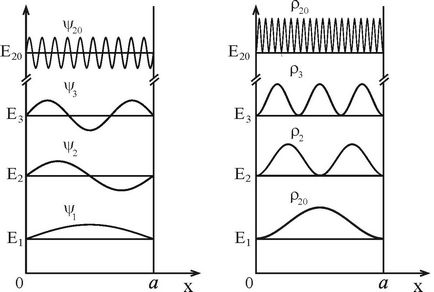
Ábra. 2.2. A spektrum energia, a hullám funkciók (a), és a valószínűség-sűrűség eloszlása (B) részecske egy végtelenül mély négyszögletes potenciálgödör