Típusai megszorozzuk projektek
probléma. megérteni a fajta szorzás
Célkitűzés: bemutatni a különböző módszerek szorzás természetes számok, amelyek nem használják az osztályban, és ezek alkalmazása számítások numerikus kifejezéseket.
célkitűzések:
1. Keresse meg és szedjük szét a különböző módon szorzás.
2. Tanulási bizonyítani néhány módszert a szorzás.
3. új módszereinek bevezetése szorzás és tanítani a diákokat, hogy használja őket.
4. készségek fejlesztése önálló munka: információkeresés, kiválasztása és kialakítása a talált anyag.
5. kísérlet „egy módja annak, hogy gyorsan”
Hipotézis: Szükséges tudni, hogy a szorzótábla?
Aktualitás: Az elmúlt években, a diákok támaszkodnak modulokat több, mint jelenleg. És ez tekinthető csak számológépek. Meg akartuk mutatni, hogy vannak különböző módszerek szorzás, hogy könnyebb lenne, hogy számít a diákok, és ez érdekes, hogy megtanulják.
BEVEZETÉS
Nem végezhet szorzata több számjegyű szám - akkor is, ha ez a kettős - ha nem emlékszik fejből minden szorzás eredményét egy számjegyű szám, azaz az úgynevezett szorzótábla ...
Különböző időpontokban, különböző emberek tulajdonában sokféleképpen szorzás természetes számok.
Most miért az egész nép használt egyik módja annak, hogy szaporodnak az „oszlop”?
Miért az emberek elhagyták a régi módon a szorzataként javára modern?
Tegye elfelejtett módon megszorozzuk a jogot, hogy létezik a mi időnkben?
Ahhoz, hogy ezekre a kérdésekre válaszolni, én a következő munkák:
1. Az információs talált néhány módszert szorzás Internet hálózat korábban alkalmazott.;
2. irodalmat, javasolt a tanár;
3. Úgy döntött, néhány példa a tanulmányozott módja, hogy megtudja a hiányosságokat;
4) azonosításához a leghatékonyabb közöttük;
5. végzett kísérletben;
6. következtetéseket levonni.
1. Keresse meg és szedjük szét a különböző módon szorzás.
Szorzás az ujjakon.
Régi orosz módra szaporodnak az ujjak az egyik leggyakoribb módja, hogy sikeresen használják évszázadok, az orosz kereskedők. Megtanulták, hogy szaporodnak egyjegyű szám az ujjak 6 és 9 Ebben az esetben ez is elég volt, hogy saját kezdeti képességek ujjat számlálás „egység”, „pár”, „három”, „négy”, „öt” és a „ten”. ujjai itt szolgál, mint egy kiegészítő számítástechnikai eszköz.
Ehhez egyrészt húzta annyi ujjait, amennyire az első tényező meghaladja az 5-ös szám, a második ugyanezt tette a második tényező. A másik volt hajtogatva ujjaival. Aztán vitték száma (összesen) hosszúkás ujjak és szorozva 10, majd a határokon szorozni a számok azt mutatják, hogy hány hullámos ujjait, és az eredményeket összegezzük.
Például, szorozza 7. 8. A példában kerül fodros ujjak 2 és 3. Ha az összeg a hajtogatott hajlított ujjak (2 + 3 = 5), és szorozzuk száma nem hajtogatott (2 • 3 = 6), és így termékként rendre számát tízes és egységek a kívánt terméket 56. Így tudjuk számítani a terméket bármely jegyű számok, több, mint 5.
Módszerek a szorzás a számok a különböző országokban
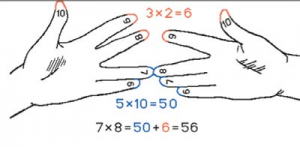
Szorzás számának 9-9 · 1, 2, ... 9 · 9 × 10 - egyszerűen szellőztetett out of memory és átalakított kézzel nehezebb túlmenően az eljárás azonban a 9-es szám van a szorzás könnyen reprodukálható "ujj". Rastopyrte ujjak mindkét kezét, és kapcsolja be a kezét, tenyérrel tőled. Értelmi rendelni ujjak egymást a számok 1-10, kezdve a kis ujját a bal oldali és a jobb oldali kisujj végződő (lásd az ábrán).
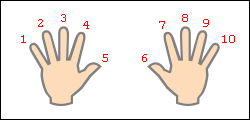
Ki találta ki a szorzást az ujjak
Tegyük fel, hogy szeretnénk, hogy szaporodnak 9 6. Fold ujját egy számot, ahány amelyhez szaporodnak kilenc. A mi példánkban, meg kell hajolni az ujját a 6-os szám száma ujját a bal oldalon a hajtogatott ujját mutatja nekünk a szám tízes a választ, hogy hány ujját a jobb - az egységek számát. A bal oldalon van 5 ujjak vannak hajlítva a jobb - 4 ujjait. Így, 9 · 6 = 54. Az alábbi ábra szemlélteti részletesen az egész elv „számítás”.
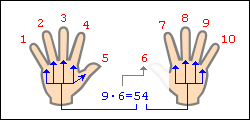
Szorzás szokatlan módon
Egy másik példa: meg kell számítani a 9 × 8 =. Az út, mondják, hogy a „számláló gép” nem feltétlenül jár ujjait. Vegyük például 10 sejtek egy notebook. Húzza ki a 8. cellában. Balról balra 7 sejtekben, jobbra - 2 sejtekben. Azt jelenti, 9 × 8 = 72. Ez nagyon egyszerű.
2 7 sejtek sejtek.
Indiai módon szaporodni.
A legértékesebb hozzájárulása a kincstár a matematikai tudás került sor Indiában. Indiánok általunk felhasznált javasolt rögzítésére szolgáló eljárást számok révén tíz szimbólumok: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Ennek alapján a módszer abban áll, a gondolat, hogy egy és ugyanaz a szám képviseli egység, több száz, vagy több ezer, attól függően, hogy milyen helyet foglal el ez a szám. Foglalt egy hely hiányában - bármely bit által meghatározott nullák, tulajdonított a számok.
Az indiánok kiválónak. Úgy jött egy nagyon egyszerű módja a szaporodásukat. Ezek szorzást végezzük, kezdve az MSB, és rögzíteni a teljes szerkezet csak egy szorzót, apránként. Amikor ez volt látható azonnal MSB befejezni a munkát, sőt kizárt kihagyva minden szám. szorzás jele még nem volt ismert, így a vizsgált tényezők között távoztak egy rövid távolságra. Például eljárás 537 szaporodnak a 6:
(300 + 3 ∙ 6 = 318) 318
(3180 +7 ∙ 6 = 3222) 3222
6
Szorzás „kis vár”.
Szorzás most tanul az első osztályban. De a középkorban, nagyon kevés elsajátította a művészet szaporodását. Ritka arisztokrata dicsekedhetett ismerete szorzótábla, annak ellenére, hogy elvégezte az európai egyetemeken.
Az évezredek során, a matematika fejlődése találták sokféleképpen szaporodnak számokat. Olasz matematikus Luca Pacioli című értekezésében „Az összeg a tudás számtani, kapcsolatok és az arányosság” (1494) szerepel nyolc különböző módszerek szorzás. Ezek közül az első az úgynevezett „kis vár”, a második nem kevésbé romantikus name „féltékenység vagy rácsos szorzás”.
Az eljárás előnye, szorzás „Little Castle”, hogy a kezdetektől a digit legjelentősebb bit, és ez fontos, ha azt szeretné, hogy becsüli gyorsan.
A számok a felső, kezdve az MSB, viszont szorozva az alsó szám egy oszlopban és a rögzített azzal a kiegészítéssel, a szükséges számú nullák. Az eredményeket ezt követően össze kell adni.

Módszerek a szorzás a számok a különböző országokban
Szorzás „féltékenység”.

„Methods of szorzás A második módszer a neve a romantikus féltékenység” vagy „Trellis szorzás”.
Először rajzoljunk egy téglalapot, négyzetekre osztva, a mérete az oldalán a téglalap megfelelnek a tizedes helyek számát a szorzó és szorzó. Ezután a tér sejtek két részre osztja, és a”..., hogy a kép, mint egy rácsos redőnyök, árnyékolók, - írta Pacioli. - Ezek a redőnyök lógott az ablakok velencei épületek, ami megnehezíti, hogy az utcán a járókelők, ül az ablak a hölgyek és az apácák. "
Szorozzuk így 347 29. Rajzolj egy táblázatot, hogy írja le a számot 347 rajta, és a jobb oldalon a 29.
Minden sorban írási termék számjegyek át ezt a cellát, és annak jobb és a tízes számjegy termék írási egy perjel és a számjegy egységek - alatta. Most add ki a számok az egyes ferde sáv, e művelet jobbról balra. Ha az összeg kevesebb, mint 10, akkor írd alá az alsó sáv számát. Ha azonban ez több lesz, mint 10, akkor írunk csak kitalálni egységek mennyisége, és a tízes számjegy hozzáadjuk a következő összeget. Ennek eredményeképpen megkapjuk a kívánt terméket 10063.
Paraszt módon szorzás.
Így véleményem szerint, a „bennszülött”, és egyszerű módja szorzás egy eljárást, amelyben az orosz parasztok. Ez a technika nem igényel ismereteket szorzótábla a 2-es szám A lényege az, hogy a szorzás bármely két szám csökken több egymást követő elválasztó egyik száma a felére, míg számának megkétszerezése másik. Bisection folytatni, amíg a saját nem kapcsol 1, párhuzamosan a duplájára száma egyaránt. Nemrég megduplázódott a számot, és adja meg a kívánt eredményt.
Abban az esetben, páratlan számú kell dobnia egy felét, és felosztják a maradékot; de az utolsó napon a jobb oldali oszlopban kell hozzá a számokat ebben az oszlopban, amely úgy áll szemben a páratlan számok a bal oldali oszlopban: az összeg a kívánt terméket
A termék az összes pár megfelelő számok azonos, így
37 ∙ ∙ 32 = 1184 1 = 1184
Abban az esetben, amikor az egyik a számok vagy páratlan számokat egyaránt páratlan, a következőképpen kell eljárni:
24 ∙ 17 = 24 ∙ (16 + 1) = 24 ∙ 16 + 24 = 384 + 24 = 408
Egy új módja a szaporodásukat.
Egy érdekes új módszer a szaporodás, amelyek a közelmúltban számoltak be. A feltaláló egy új rendszer az orális figyelembe PhD Vaszilij Okoneshnikov kimondja, hogy a személy képes memorizálni egy hatalmas raktár információt, ami a legfontosabb -, hogyan lehet rendezni az adatokat. A véleménye szerint a tudós, a legelőnyösebb ebben a tekintetben kilences rendszer - minden adat csak kilenc sejtek elrendezni, gombok a számológép.
Tekinthető nagyon egyszerű egy asztalra. Például, hogy szaporodnak a szám 15647 5. A táblázat megfelelő öt válasszon megfelelő számot a számjegyek száma sorrendben: egy, öt, hat, kvartett és a hetedik. Kapunk: 05 25 30 20 35
A bal oldali ábra (a mi példánkban - nulla) változatlanul hagyja, és a következő számok összeadódnak párban az első öt két, öt hármas, nulla-kettő, nulla és három. Az utóbbi ábra azt is változatlan.
Ennek eredményeképpen megkapjuk: 078235. A szám 78235 az a szorzás eredményét.
Ha kiderül száma több mint kilenc, az első számjegy hozzáadjuk az előző ábrán az eredmény, a második van írva, hogy „ő” helye a további két szám.
Szorzás grafikus módszerrel (lineáris, Kína)
Peremnozhim kétjegyű szám: 15 * 23
1. lépés: Az első szám 15:
Rajz az első szám - egy sorban.
Rajz a második számjegy - öt sor.
2. lépés: A második szám 23:
Rajz az első számjegy - a két sor.
Rajz a második számjegy - három sor.
3. lépés.
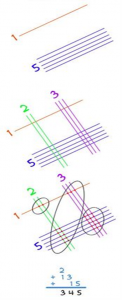
4. lépés: Az eredmény - 345
A stopper beállítani az időt töltött a megoldás például az egyes figyelembe vett módszer.
A munka ebben a témában, azt tapasztaltam, hogy van körülbelül 30 különböző, szórakoztató és érdekes módon szaporodnak. Néhány különböző országokban eddig. Azért választottam néhány érdekes módon. De nem minden módszer használata egyszerű, különösen, ha szorozni több számjegyű számokkal.