Aszimptotikus összetettsége az algoritmus
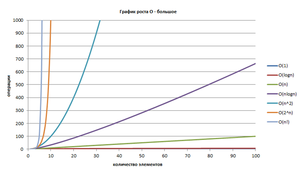
A műveletek száma az algoritmusok különböző összetettségű
Aszimptotikus összetettsége az algoritmus - a módszer értékelésére számítási komplexitását „akár egy állandó” használt algoritmus komplexitás elmélet. „Big-O” általában írva a jelölést.
Széles körben használják pontos értékelést összetettsége szempontjából elemi műveletek gyakran összetett (beleértve attól is függ, hogy mit veszünk az elemi művelet - egy akció egy adott programozási nyelv, a CPU órajel), és nincs értelme a nagy mennyiségű input adatok, ha része a lassú idő függvényében gyakorlatilag megszűnik mértékének növelése végrehajtott munka.
A leggyakrabban használt aszimptotikus becsült idő a fenti algoritmus, rögzítésre O (f (n)), ahol n - az összeget a bemeneti adatokat. Ha vesszük az idő függvényében az algoritmus mennyiségétől függően a bemeneti adatok például az F (n), akkor azt mondhatjuk, hogy bizonyos idő után a N minden n> N az | F (n) | <= |N*f(n)|. иными словами, с некоторого момента функция F(n) растет не быстрее. чем N*f(n), где N — константа.
A becslések szerint az algoritmusok bonyolultsága:
- Logaritmikus összetettsége - független a bemeneti adatok n, mint az N * log (n), különösen a komplexitás önmagában rendelkezik a keresési művelet indexált tömb, gyors erekció egy tetszőleges teljesítmény. A gyakorlatban, több gyakori szövődménye N * N * log (n).
- Polinom összetettsége - független a bemeneti adatok n, mint az N * N ^ c, ahol a c - valamilyen különleges mértékben. Jelezte csak a legnagyobb hatalom a polinom, n növekedése kisebb mértékben megszűnik jelentősen befolyásolja. Például használhatók kettős brute tömb van komplexitása O (Nl), végrehajtása Schulze eljárás jelöltek n - O (N³).
- Exponenciális komplexitás - attól függően, hogy a bemeneti adatokat n, mint az N * e ^ n. Algoritmusok segítségével a komplexitása próbálják elkerülni ezt az összetett problémát grafikonokon, összetett kereséseket több táblázatok a MySQL, és így tovább. D.
Lehetséges és nagyobb komplexitás, például N * n.