minimalizálása kártya módszer
Ennek egyik módja grafikus ábrázolása a FAL kisszámú változók - használata Karnaugh térképeket. Ezek különböző - Veitch térkép, amely úgy van felépítve, mint egy kocka egy síkban sweep. Ebben az esetben a csúcsai a kocka térkép által képviselt sejtek, amelynek koordinátái megegyeznek a koordinátákat a megfelelő csúcsait a kocka. Karnaugh térkép is tele van, mint az igazság táblázat: Az egyes cellákban, amely megfelel a beállított elhelyezni függvény értékét. A változók helyezni a térképen, hogy az átmenet az egyik cellából bármelyik szomszédos, csak egy változót kell változtatni. Az alsó kártyák száma minősülnek mellett a felső sorban, és a bal sávban - a jobb oldalon.
Karnaugh Maps:
2 változók 3 4 változók változók.
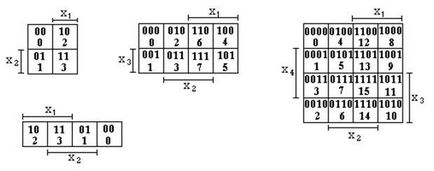
Ha azt szeretnénk, hogy egy Karnaugh térkép minden funkciót, először meg kell írni a funkciót a NDF. Minden egyes tagja, amely úgy tűnik, ebben a formában, definiáljuk a térképen a Carnot-1 a megfelelő sejt. Ezután csoport az egységek a megfelelő mezőkbe, vázolja zárt vonalakon. A tanuló a térképeket vázolt területeken van az, hogy ha két szomszédos sejt tartalmaz 1, akkor az egyiket mindig távolítsa el a változó, azaz a változó, amelyre ez az inverzió a következő szomszédos cellában. Tekintsük a példák a funkciók 2, 3 vagy 4 változók.
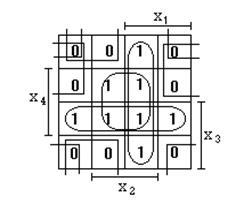
Jelenleg a következő Karnaugh térképen:
Aztán formájában minimum funkció is képviselteti magát:
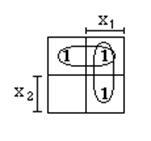
Ehhez a funkcióhoz Karnaugh térkép fog kinézni:
Miután minimalizálása get:
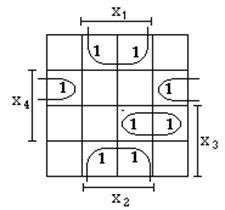
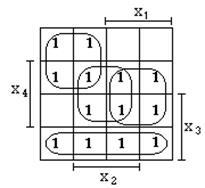
Egyértelmű, hogy a logikai függvény az előző példában is képviselteti formájában minimum és más lehetőségeket ötvöző „1” a másik oldalon.
Karnaugh térkép a változók száma n> 4 épülnek fel azonos (szempontjából kijelölésének primer oldalán értelemben) térképek a négy változó.
Két Karnaugh térképek a négy változó lesz az úgynevezett szomszédos, ha van egy közös oldala. Cells található ugyanabban a helyzetben a szomszédos lapok a négy változó a közelben vannak, mint felelnek meg a szomszédos mintermy.
Például, az n = 5
Szomszédos sejtek itt: 0, 16, 1 és 17, 7 és 23, 14 és 30, 8 és 24, stb
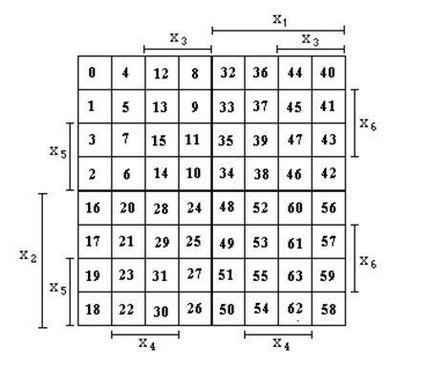
Vannak szomszédos sejtek: 0 és 32, 0, 16, 5 és 37, 5 és 21, 14 és 30, 14 és 46, stb De 0 és 48, a 18 és 34, 15 és 63, stb Ezek nem szomszédosak.
Példa. Kis méret FAL:
Összhangban a fenti, megkapjuk Karnaugh térkép, amely látható, ábra. 2.4.
És minimalizálásával get:
Elég nyilvánvaló, hogy a helymeghatározás a mezőváltozók más módon, de a szabályok betartása elkészítésének térképek Carnot kapjon azonos minimális funkciót. (Az a kifejezések száma és hosszúsága).
Példa. Kis méret FAL:
Kitöltése Karnaugh térkép n = 6, megkapjuk:
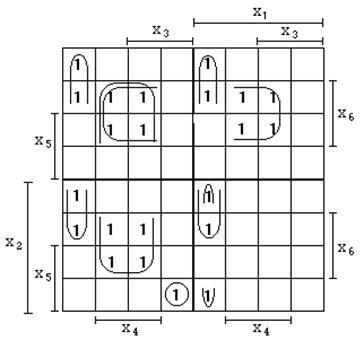
minimalizálják az eredmény kerül bemutatásra ebben az esetben:
Karnaugh térképeket használnak, és a minimális CNF. Ez következik a dualitás elve és a dualitás törvényeket. Megmutatjuk ezt egy példával.
Tegyük fel, hogy van egy FAL.
Minimalizálása segítségével Carnot (2.5 ábra) kártya fogadására:
Akkor mi ebben az esetben a következő összefüggés:
ahonnan megkapjuk alapján kettősség: