Előadás a központi szimmetria
2. Mi az a szimmetria? Milyen szimmetria úgynevezett központi? Példák a központi szimmetria.

3 meghatározása szimmetria: két pont, A és A1 jelentése a nevezett szimmetrikus az O pont, ha O - közepe szegmens AA1. Az O pont minősül szimmetrikus magára. Meghatározása szimmetria: Két pont, A és A1 nevezzük szimmetrikus az O pont, ha O - a középpontját AA1. Az O pont minősül szimmetrikus magára.

4 Példa: ábra pontokat M és M1, N és N1 szimmetrikusak képest O pont, valamint a P és Q pontok nem szimmetrikus tekintetében ezen a ponton példa: ábra pontokat M és M1, N és N1 szimmetrikusak képest O pont, valamint a P és Q pontok nem szimmetrikus ezen a ponton

5 elképzelni a rajzban.
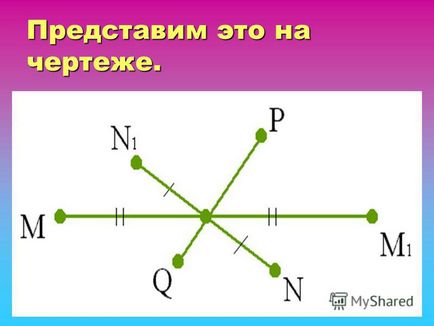
6 meghatározása központjában szimmetria: Az ábra az úgynevezett szimmetrikus az O pont, ha minden pont szimmetrikus formálja ő pont képest pont O is tartozik ez a szám. Azon a ponton az úgynevezett központja szimmetria az ábra. Azt is mondta, hogy ez a szám van egy központi szimmetria. A szám az úgynevezett szimmetrikus az O pont, ha minden pont szimmetrikus formák ő pont képest pont O is tartozik ez a szám. Azon a ponton az úgynevezett központja szimmetria az ábra. Azt is mondta, hogy ez a szám van egy központi szimmetria.

7. ábra példákat alakú, és van egy központi szimmetria. Csak egy alak rendelkező központi szimmetria egy kör és egy paralelogramma.

8. központja szimmetria kör a kör közepén

9 És központja szimmetria paralelogramma - a metszéspontja az átlók.

10 Közvetlen is van egy központi szimmetria, de ellentétben a kör és egy paralelogramma, amelyeknek csak egy központja szimmetria (D pont az ábrán) egy egyenes vonal végtelen sok - bármely pontján a vonal közepén szimmetria. Egy példa a számok, anélkül, hogy a központ a szimmetria, egy háromszög.

11 Példák a központi szimmetria.
12
13