Még a véges körülveszi egy végtelen sorozat, és a korlátlan határok jelenik meg, ezért a lélek

Még a véges körülveszi egy végtelen sorozat
És a korlátlan határokig,
Tehát a lélek mérhetetlen lakozik minutia
És a legszűkebb határok no limit itt.
Micsoda öröm, hogy felismerjük a perc a végtelenben!
A hatalmas érzékelni a kis, milyen isteni!

Amint az a végső végtelen sorokban,
Hogy végtelen hirtelen korlátozott,
Tehát a szellem a mérhetetlen életek a részletek
És szoros határok jogok határtalan.
Micsoda öröm, hogy képes legyen megkülönböztetni percet végtelenig!
Milyen isteni, hogy a végtelenség a kicsi!
Jacob Bernoulli. „Feltételezések Art”

A sírfelirat a sír a spirál és Jakob Bernoulli

1692-ben Jakob Bernoulli megmutatta az első jelei a tuberkulózis, ahonnan halt meg 1705. Tiszteletére Jacob és Johann Bernoulli nevű kráter a Holdon.

Tanulmányozta az elmélet a valószínűség alapján a könyv a Huygens „A számítás a szerencsejátékban”, ami még nem volt a fogalma, a valószínűség (ez helyettesíti a számát kedvező esetben). Jacob Bernoulli be egy jelentős része a modern koncepciók valószínűségszámítás és megfogalmazta az első változata a nagy számok törvénye. Jacob Bernoulli készített monográfia a területen, de nem volt ideje, hogy kiadják. Ezt posztumusz megjelent, 1713-ban, testvére Miklós, a cím alatt: „The Art of feltételezések» (Ars conjectandi). Ez informatív értekezést valószínűség, statisztika, és azok gyakorlati alkalmazása, az eredmény a kombinatorika és a valószínűségszámítás a XVII században. Név Jacob fontos valószínűségszámítás, Bernoulli eloszlás.
Jacob Bernoulli is megjelent munka különböző kérdésekben a számtan, algebra, geometria és a fizika.

Bernoulli eloszlás
Azt hiszem, senki diák, hogy egy tanfolyam a valószínűségszámítás, aki nem tudja, mi a Bernoulli eloszlás.
Bernoulli eloszlás valószínűségszámítás és a matematikai statisztika - diszkrét valószínűségi eloszlás, amely modellezi a véletlen kísérlet egy tetszőleges jellegű, ha előre ismert a valószínűsége a siker vagy kudarc.
A valószínűségi változó X egy Bernoulli-eloszlás, ha azt csak a két érték 1 és 0 valószínűséggel p és q = 1-p, ill. tehát:
P (X = 1) = P,
P (X = 0) = q.
Azt mondjuk, hogy az esemény X = 1 felel meg a „siker”, és az X = 0 „hiba”. Ezek a nevek feltételes, és attól függően, hogy az adott alkalmazás lehet helyettesíteni az ellentétek.
Pillanatok Bernoulli eloszlás
E [X] = p,
D [X] = pq.
Általában ez könnyen belátható, hogy
E [X ^ n] = p, bármilyen fokú n.

Bernoulli-számok
Bernoulli-számok - sorozata racionális számok `B_0, B_1, B_2. `First tekinthető Jacob Bernoulli kapcsolatban a számítás összege egymást követő pozitív egész épültek azonos mértékben:

ahol - a binomiális együttható.
tulajdonságok
- Minden Bernoulli-számok páratlan számok, kivéve `B_1`, nulla, és a jelek számok Bernoulli számok akár alternatív.
- Bernoulli számok értékei polinomok Bernoulli `B_n (x)`, ha `x = 0`:` B_n = B_n (0)”.
Bernoulli-számok gyakran jönnek a tágulási tényezőjük elemi függvények hatványsorba.

Írásbeli 1713

Bernoulli lemniscate
Lemniszkáta (lat lemniscatus -. «Szalagos") - sík algebrai görbe érdekében 2n, ahol a termék a távolságok minden egyes pontot n, hogy az adott pontok (gócok) állandó.

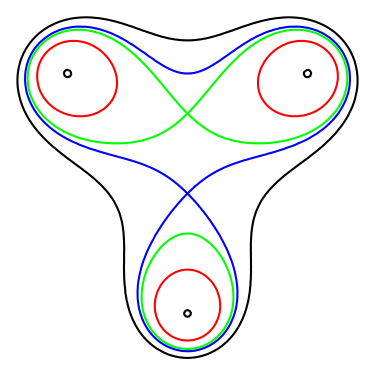
Lemniscate három fix fókusszal

példák
- Lemniszkáta egy fókusz (n = 1) egy r sugarú kör, és a két gócok - Cassini ovális.
- A speciális esete az ovális Cassini egy lemniszkáta nevében a svájci matematikus Jacob Bernoulli, aki kezdte tanulmányozni lemniscates.

Lemniszkáta - sík algebrai görbe. Ez úgy definiáljuk, mint a pontok helye, amely a termék a távolságok két adott pont (gócok) állandó és egyenlő a tér közötti távolság felének a gócok.
Lemniszkáta alakú nyolcas vagy végtelen jel. Az a pont, amelynél a lemniszkáta metszi önmagát, úgynevezett csomópontként vagy dupla.

Lemniscate és trükkök

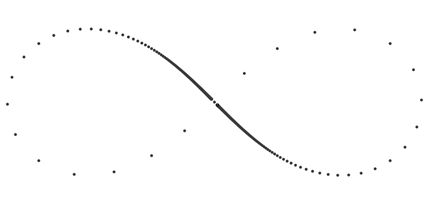
A sűrűsége a pontokat a görbe egyenletes változása a paraméter

Gravitációs ingatlan lemniscate

Anyagi pont mozog az intézkedés alapján a mozgató egységes gravitációs mező, az ív fut át ​​időben a megfelelő húrt (lásd. Ábra). Feltételezzük, hogy a lemniszkáta tengelye szöget zár 45 o a vektor a térerősség, és a központ a lemniszkáta egybeesik a kezdeti helyzetben a mozgó pont.

Az épület lemniscate segítségével metsző

Csuklós építési módszerek

Közös eljárás